Pencereler ve Spektral Sızıntı (Leakage)
Bu makalede, sızıntıya neyin neden olduğu, neye benzediği ve Fourier Dönüşümü gerçekleştirmeden önce zaman alanındaki bir sinyali yumuşatarak sızıntının etkilerini azaltmak için pencerelerin nasıl kullanılacağı açıklanmaktadır.
Sinüs Dalga Örneği
Bir sinüs dalgasını örnek alın. Analizörünüzün, Şekil 1’de gösterildiği gibi 1Hz frekans çözünürlüğüne neden olacak bir Hızlı Fourier Dönüşümü (FFT) yapmak üzere ayarlandığını varsayalım. Frekans çözünürlüğü ayarı, bilgisayarın yalnızca her 1Hz’de veri görüntüleyebileceği anlamına gelir.
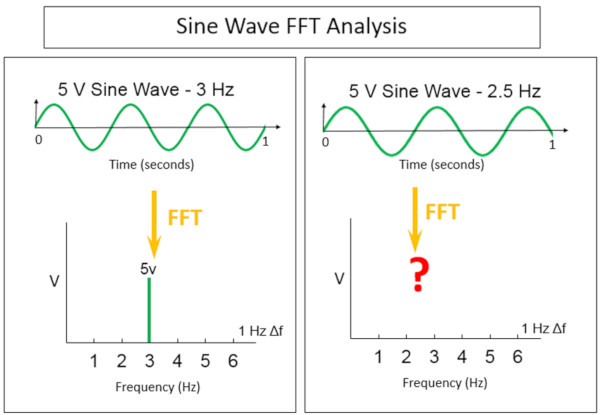
Şekil 1’den aşağıdakiler gözlemlenebilir:
– Sol tarafta, frekans alanında üç Hertz sinüs dalgasını görüntülemekte sorun yoktur. Üç Hertz spektral çizgisinde, genlik tam olarak 5 Volttur. Üç Hertz, 1Hz frekans çözünürlüğünün tam sayı katıdır.
– Sağ tarafta, 2.5 Hertz sinüs dalgasının nasıl temsil edilebileceği net değil. Bilgisayar, veri toplama ayarları nedeniyle, yalnızca her 1Hz’de veri görüntüleyebilir. Verilerin 2,5 Hertz’de görüntülenmesi bir olasılık değildir.
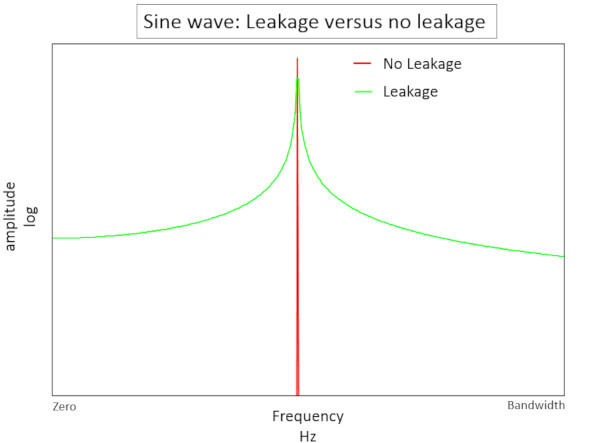
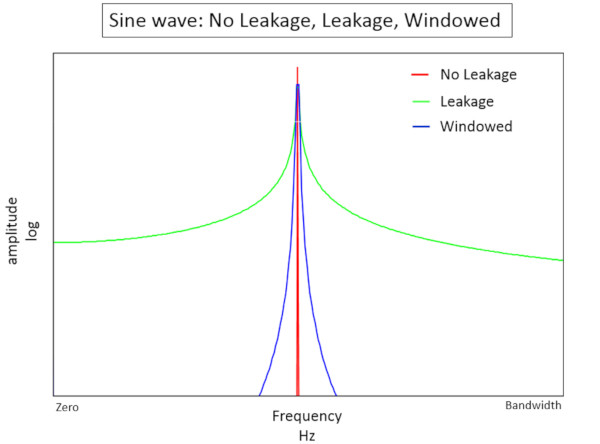
Veriler 2.5 Hertz’de görüntülenemediğinden, 2.5 Hertz sinyali Şekil 2’de gösterildiği gibi sıfır Hertz’den tam bant genişliğine sızacaktır.
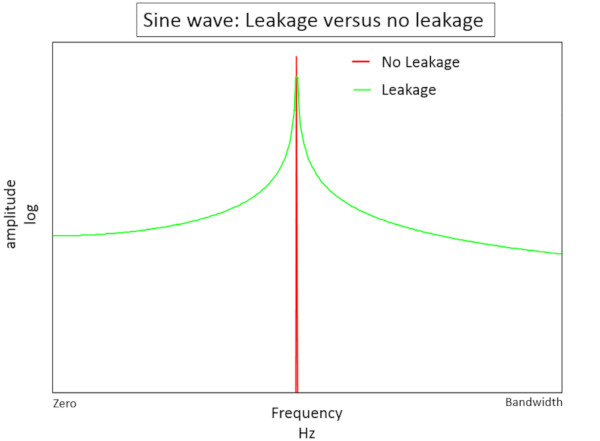
Sızıntı olan bir sinyal (Şekil 2’de yeşil), sızıntı olmayan bir sinyale (Şekil 2’de kırmızı) göre daha düşük genliğe ve daha geniş bir frekans tepkisine sahiptir. Bu, frekans alanında sinyalin doğru şekilde ölçülmesini zorlaştırır.
Sızıntı (Leakage)
Sızıntı neden tüm frekans aralığını etkiler? Bu durum, sinyalin, ölçüm zaman çerçevesine göre periyodik olup olmadığı ile ilgilidir.
Periyodik Sinyaller
Periyodik bir sinyal belirli özelliklere sahiptir.Şekil 3’teki ölçümü düşünün.
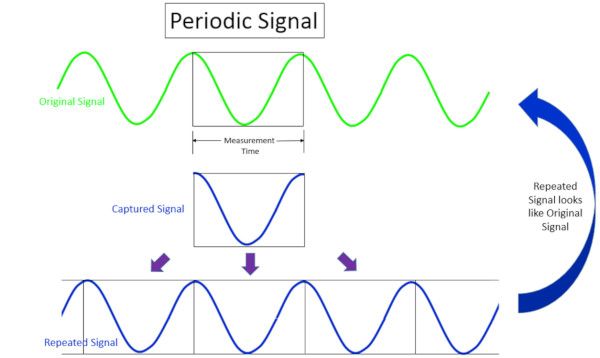
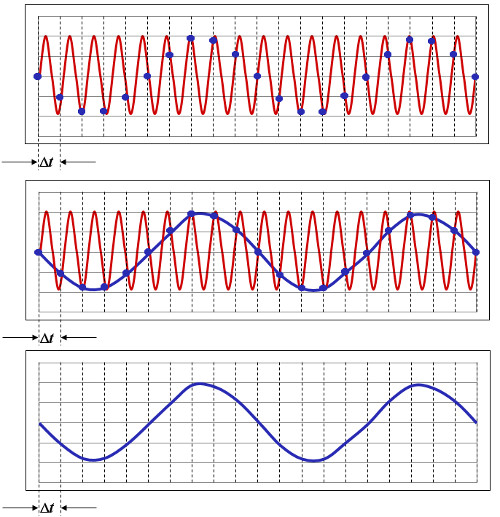
Sinüs dalgasının ölçümü yapılır. Veri toplama için belirtilen çerçeve boyutuna (ölçüm süresine) bağlı olarak, orijinal sinüs sinyalinin sadece küçük bir miktarının yakalandığına dikkat edin. Buna Şekil 3’te “yakalanan sinyal” denir.
Daha sonra “yakalanan sinyal” tekrarlanır ve uç uca eklenir, buna Şekil 3’te “tekrarlanan sinyal” denir. Tekrarlanan sinyal orijinal sinüs dalgasına benziyorsa, yakalanan sinyal periyodiktir.
Yakalanan sinyal neden tekrar tekrar kopyalanır? Bu, FFT’nin dayandığı Fourier Dönüşümü (Denklem 1) üzerindeki integral aralığından kaynaklanmaktadır:
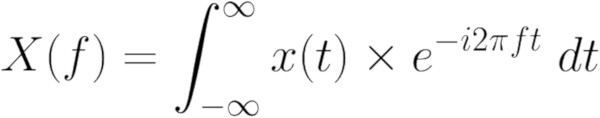
İntegralin aralığı eksi sonsuzdan artı sonsuza gider, bu nedenle bu denklemi sağlamak için küçük kesilmiş aralığın tekrarlanması gerekir.
Böylece FFT algoritması, Fourier Dönüşümü’nü gerçekleştirmek ve bir frekans spektrumu üretmek için az miktarda yakalanan veriyi alır ve tekrarlar. Bu sinyalin önceki ve sonraki tüm zamanlar için tekrarlandığını varsayar.
Bu durumda, sinyal periyodiktir ve elde edilen frekans spektrumunda sızıntı (leakage) oluşmayacaktır.
Periyodik Olmayan Sinyaller
Sadece ölçüm süresi küçük oranda değiştirilerek, yakalanan sinyal Şekil 4’te gösterildiği gibi periyodik olmayacaktır.
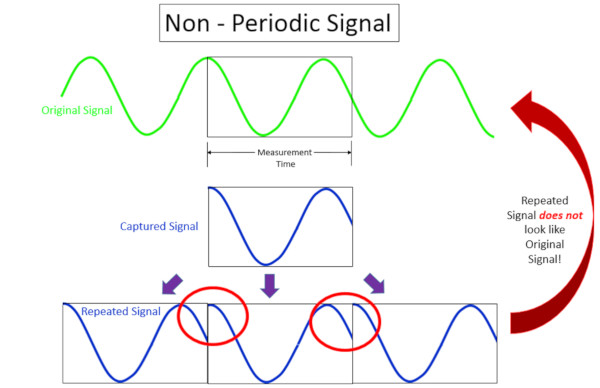
Yakalanan her sinyalin sonunda ani geçişler vardır. Şekil 4’te kırmızı ile daire içine alınmış bu keskin geçişler geniş bir frekans tepkisine sahiptir. Zaman alanındaki kısa geçici sinyaller, Şekil 5’te gösterildiği gibi yüksek, geniş bant frekans içeriği üretir.
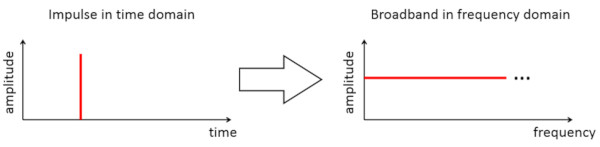
Sonuçta elde edilen spektrum yeşil renkte Şekil 6’da gösterildiği gibi geniş bant yanıtı ve sinüzoidal yanıta sahip olacaktır.
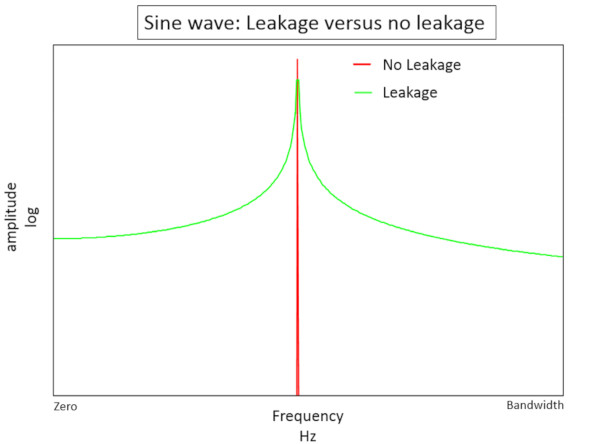
Çoğu zaman elde edilen sinyal ölçüm süresi ile periyodik değildir. Çalışan bir motor veya pompa normalde ölçüm süresinin tam katı olan frekans içeriği üretmez. Motor veya pompanın çalışması veri toplama ayarlarından etkilenmez.
Kontrollü deneylerde,sarsıcı ile yapılan bir modal analiz gibi, ölçüm, sızıntıyı ortadan kaldırmak için bir kaynak ile senkronize edilebilir.
Ölçümlerin büyük çoğunluğu periyodik olmayan sinyallere sahip olacağı için, bu durumlarda “Sızıntının nasıl en aza indirileceği?” sorusu akla gelir.
Pencereler
Sızıntıyı azaltmak için, verilere pencere adı verilen matematiksel bir işlev uygulanır. Pencere, yeniden oluşturulan sinyaldeki keskin geçişi olabildiğince azaltmak için tasarlanmıştır.
Pencereler tipik olarak sıfır değerinde başlayan, bir değere hareket eden ve sonra bir kare üzerinde sıfır değerine dönen işlevler olarak şekillendirilir. Yakalanan sinyal, Şekil 7’de gösterildiği gibi pencere ile çarpılır.
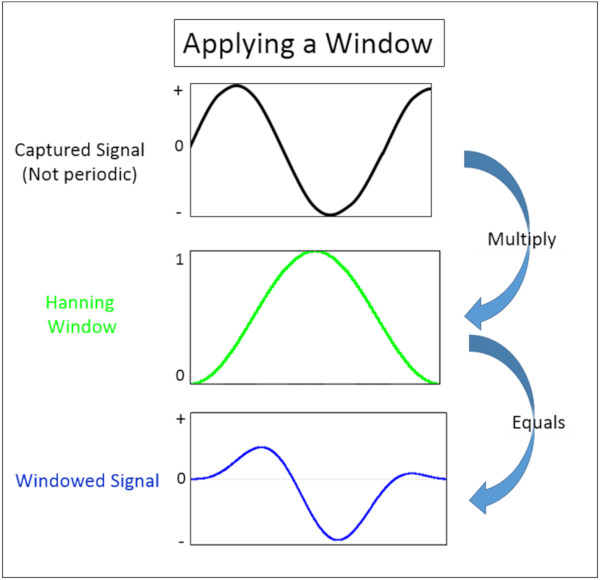
Pencerelenen sinyal daha sonra Şekil 8’de gösterildiği gibi tekrarlanır ve uç uca eklenir. Tekrarlanan sinyal orijinal sinyale uymasa bile, keskin geçişler giderildiğine (sarı daire içine alınmış) ve yumuşatıldığına dikkat edin.
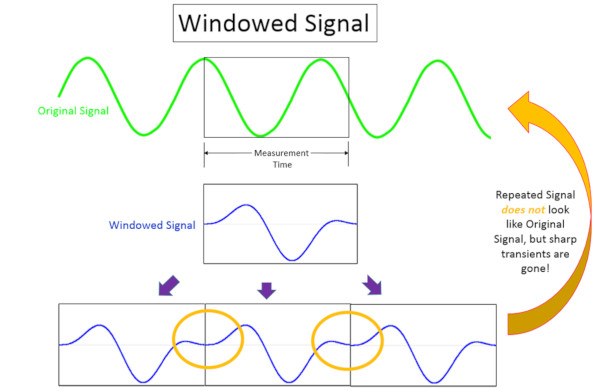
Keskin geçişler azaltıldığı ve düzeltildiği için, spektral sızıntının geniş bant frekansı da azalır.
Sızıntıyı Azaltma Avantajı
Orijinal sinyalle uyuşmuyorsa, sinyali neden bir pencere ile çarpalım?
Faydası, yakalanan sinyalin mükemmel bir şekilde kopyalanması değildir. Ana fayda, sızıntının artık ölçümün tüm frekans bant genişliğini etkilemek yerine daha küçük bir frekans aralığında sınırlanmasıdır.
Bunun iyileştirilmesi, sızıntının frekans aralığını Şekil 9’da gösterildiği gibi düşürmektedir.
Sızıntı daha küçük bir frekans aralığına yayıldığında, RMS gibi analiz hesaplamaları yapmak daha doğru sonuçlar verir.
Simcenter Testlab’da, doublex cursor, RMS hesaplamak için kullanılabilir. Spektral sızıntı azaldığı için, bir operatörün cursorlarını daha dar bir frekans aralığına yerleştirmesi daha kolaydır.
Şekil 10’da sızıntı bütün frekans aralığının üzerinde olduğu için, double X cursorla penceresiz sinüs dalgasının sınırlı bir frekans aralığı üzerinden, uygun RMS genlik hesaplamak imkansızdır. Bu nedenle RMS genliği doğru değildir.
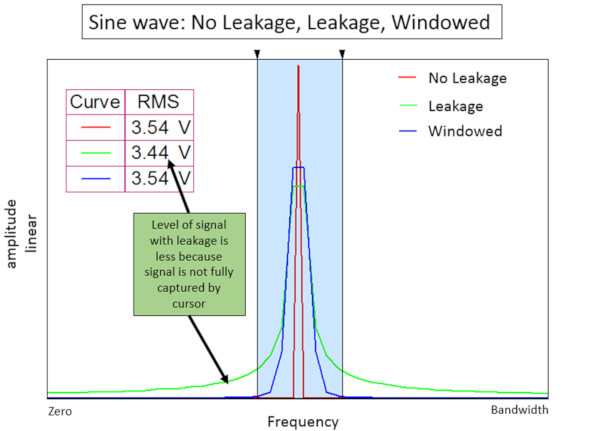
Gerçekte olan ölçümlerde, genellikle birçok farklı frekans vardır. Bir pencere uygulanmadan, bu frekanslar birbirine sızarak imkansız olmasa bile, tekil piklerin gerçek genliğinin belirlenmesini çok zorlaştırır. Şekil 11’de, pencereli ve penceresiz iki farklı ton sızıntı üst üste binmiştir.
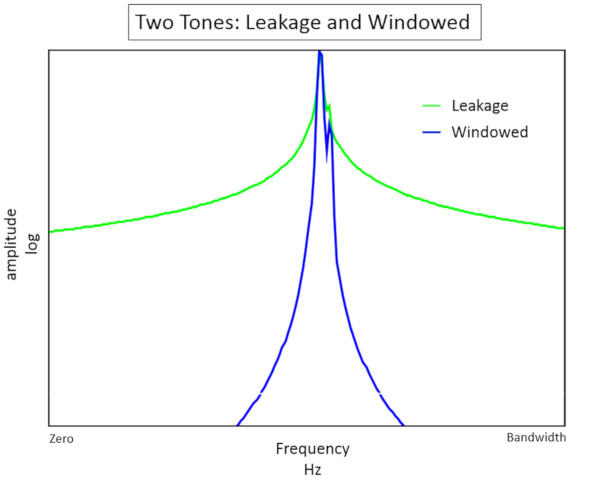
İki yakın aralıklı sinüs formu durumunda, pencere her formuayırt etmeyi kolaylaştırır, böylece uygun bir analiz yapılabilir.
Pencere Çeşitleri
Her biri belirli durumlar için optimize edilmiş farklı pencere çeşitleri vardır. Bazı pencereler şunları içerir:
– Hanning- Genel veri analizi, frekans ve genlik doğruluğu arasında iyi dengeleme için kullanılır.
– Flattop- Genlik için mükemmel doğruluk, genellikle kalibrasyonda kullanılır.
– Tukey- Anlık olaylar için kullanılır.
– Exponential- Çekiç darbeli modal testinde kullanılır, ölçüme yapay sönümleme eklemeye dikkat edin.
– Uniform- “Penceresiz” demenin başka bir yoludur.
Ölçüm durumuna bağlı olarak uygun pencere uygulanabilir.
Sonuç
Spektral sızıntı, pencereler uygulanarak çözülebilen dijital sinyal işlemede bir zorluktur:
– Sızıntı, periyodik olmayan verilerin dijital Fourier dönüşümü ile oluşur.
– Sızıntı, sinyalin, ölçümün tüm frekans aralığında yeniden dağıtılmasına neden olur.
– Pencereler, zaman alanı sinyalini yumuşatarak sızıntının etkilerini en aza indirmeye yardımcı olabilir, ancak sızıntıyı tamamen ortadan kaldıramaz.
Uygulama hakkında sorularınız için DTA Mühendislik Test Bölümü mühendisleriyle iletişime geçebilirsiniz.