Fourier Dönüşümü kullanarak zaman alanındaki verileri frekans alanına çevirirken spektral sızıntıyı (leakage) azaltmak için kullanılan birkaç farklı pencere (window) tipi vardır.
Her pencere özel bir amaç için tasarlanmıştır. Aşağıdaki pencerelerin ayrıntıları bu makalede ele alınacaktır:
– Hanning
– Flattop
– Uniform
– Tukey
– Exponential
Makale boyunca ölçüm süresi terimi, tek bir ortalama veya bir veriye FFT uygulamak için geçen süreyi ifade eder. Ölçüm süresi, çerçeve boyutu olarak (frame size) da adlandırılabilir.
Arkaplan: Periyodik ve Periyodik Olmayan
Her pencerenin özelliklerine girmeden önce, periyodik veya periyodik olmayan bir şekilde yakalanan sinyallerin ışığında spektral sızıntıyı anlamak faydalıdır. Ölçüm süresi tarafından nasıl yakalandığına bağlı olarak herhangi bir sinyal verisi periyodik veya periyodik olmayabilir.
Ölçüm verilerinde bir Fourier Dönüşümü gerçekleştirirken, pencereleme periyodik ve periyodik olmayan verileri farklı şekilde etkiler:
– Periyodik (Pencere Gerektirmez): Periyodik bir şekilde yakalanan sinyal bir pencere gerektirmez ve sonuçta ortaya çıkan Fourier Dönüşümünün sızıntısı yoktur. Bir pencere uygulamak, Fourier dönüşümünü değiştirir ve hatta başka türlü sızıntı olmayacağı yerlerde spektral sızıntı yaratır.
– Periyodik Olmayan (Pencere Gerektirir): Pencereler, spektral sızıntıyı azaltmak ve periyodik sonuçlara yaklaşmak için periyodik olmayan bir şekilde yakalanan sinyallerde kullanılır. Bir pencere, periyodik olmayan bir sinyalde bulunan sızıntıyı en aza indirebilir, ancak ortadan kaldıramaz.
Ölçüm süresini değiştirerek, aynı sinyal, Şekil 1 ve 2’de gösterildiği gibi periyodik veya periyodik olmayacak şekilde toplanabilir.
Bir ölçüm sinyali periyodik bir şekilde yakalandığında, çoğaltılır ve birçok kez uç uca eklenirse, orijinal sinyale özdeş olacaktır (Şekil 1).
Ölçülen verinin orijinal sinyalin tamamını temsil ettiği varsayıldığından sinyal matematiksel olarak tekrarlanır ve uç uca eklenir.
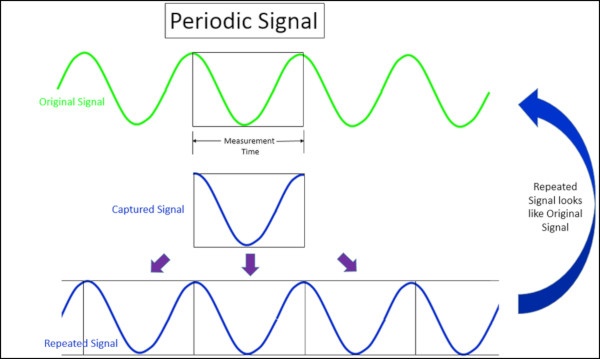
Periyodik bir sinyal için, yakalanan sinyalin Fourier Dönüşümü, Şekil 3’te gösterildiği gibi frekans alanında herhangi bir sızıntıya sahip olmayacaktır. Sinyali gereksiz şekilde bozacağından ve bir spektral sızıntı oluşturacağından burada bir pencere önerilmez.
Farklı bir ölçüm süresine sahip aynı sinüs dalgası, Şekil 2’de gösterildiği gibi periyodik olmayan yakalanmış bir sinyale yol açar.
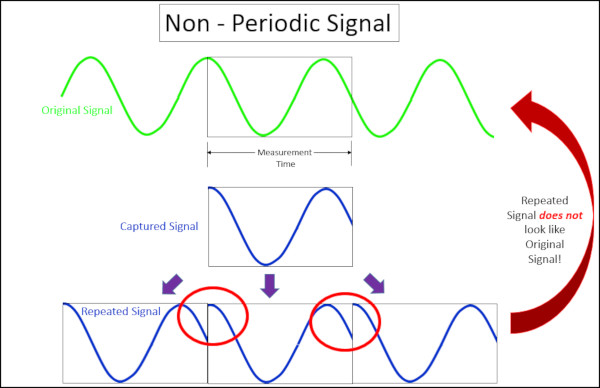
Burada, yakalanan sinyal tekrarlandığında, orijinal sinüs dalgası sinyali yeniden oluşturulmaz. Tekrarlandığında, çeşitli geniş bantetkisine sahip anlık yükseliş-düşüşler (Şekil 2’de kırmızı ile daire içine alınmış) oluşmaktadır. Bu durumlar, Şekil 3’te gösterildiği gibi geniş bant yanıtı veya sızıntı oluşturur.
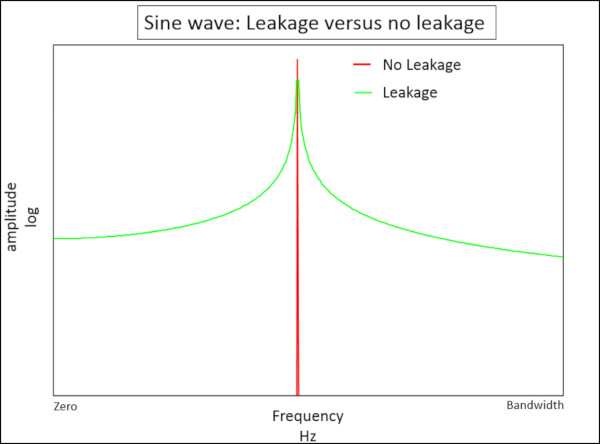
Pencereler, frekans alanındaki bu sızıntı etkisini en aza indirmek için kullanılır.
Makalede sunulan örneklerin birçoğunda, bir pencerenin periyodik ve periyodik olmayan veriler üzerindeki etkileri frekans alanındaki grafiklerde görüntülenmiştir.
Hanning
Operasyonel gürültü ve titreşim ölçümleri yaparken, Hanning penceresi yaygın olarak kullanılır.
Birçok operasyonel sinyal, Şekil 4’te gösterildiği gibi doğada rastgeledir. Rastgele sinyallere örnek vermek gerekirse, bir yolda sürüş ile üretilen ses, bir pompa / motor çalışırken oluşan titreşim veya akan suyu olan bir musluğun sesi olabilir.
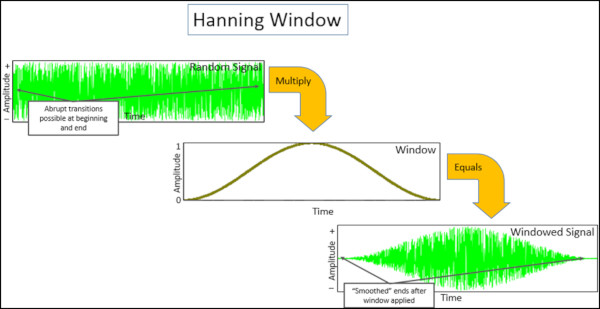
Rastgele veriler, zaman bloğunun başında ve sonunda ani kesilme nedeniyle spektral sızıntıya sahiptir. Bu sinyal periyodik değildir. Ölçüm süresini değiştirerek yakalanan rastgele sinyalin periyodik olmasını sağlamanın bir yolu yoktur. Rastgele bir sinyal birçok farklı frekanstan oluşur ve veri toplama süresi sızıntı yaratmadan bazı frekansları yakalamak için ayarlanmış olsa bile, diğer frekanslar periyodik olmayabilir.
Hanning pencereleri, özellikle diğer pencerelerin etkileriyle karşılaştırıldığında, elde edilen frekans spektrumunun frekans çözünürlüğü ve genlik doğruluğu üzerinde orta derecede etkiye sahip oldukları için genellikle rastgele verilerle kullanılır. Bir Hanning penceresinin maksimum genlik hatası%15 iken, sızıntı tipik olarak orijinal sinüs dalga sinyalinin her bir tarafındaki 1.5 spektral çizgiyle sınırlıdır.
Maksimum genlik hatası%15, pencere düzeltme faktörleri uygulandığında bile geçerlidir. Hanning penceresi periyodik olarak yakalanan sinüs dalgası üzerinde kullanılırsa hata%0 olur. Maksimum%15 hata sinüs dalgası iki spektral çizginin yarısı ortasında kaldığında meydana gelir. Sinüs dalga frekansı iki spektral çizgi arasındaki mesafenin dörtte biri olsaydı, genlik hatası%7,5 olurdu.
Hanning penceresi sıfır değerinde başlar ve sıfır değerinde biter (Şekil 5). Pencerenin ortasında 1 değeri vardır. 0 ile 1 arasındaki bu kademeli geçiş, ölçülen sinyali pencere ile çarparken genliklerde yumuşak bir değişiklik sağlar ve bu da spektral sızıntıyı azaltmaya yardımcı olur.
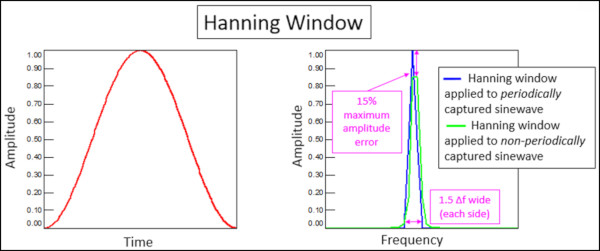
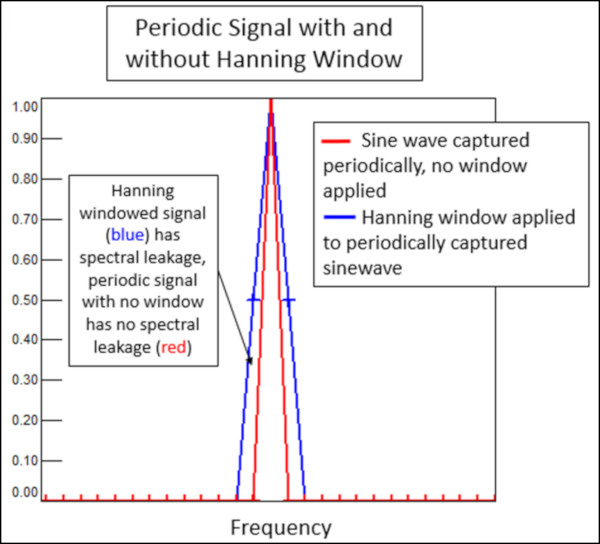
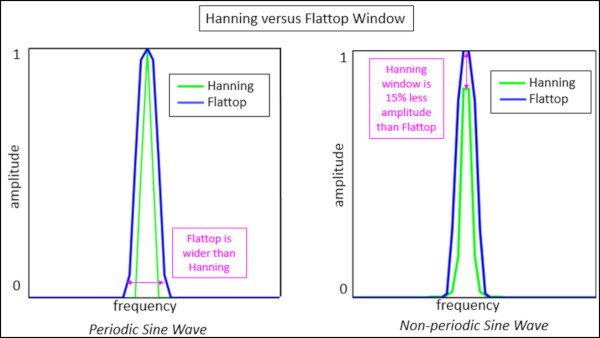
Şekil 6’da,Hanning penceresi uygulanmış ve uygulanmamış bir periyodik sinüs dalgası gösterilmiştir. Hanning penceresinin (veya herhangi bir pencerenin) periyodik bir sinyale uygulanması sızıntıya neden olur. Şekilde, Hanning pencereli (mavi) sinüs dalgası frekansta orijinal sinyalden (kırmızı) daha geniştir.
Şekil 7’de gösterildiği gibi periyodik olmayan bir sinyale bir Hanning penceresi uygulandığında, sızıntı büyük ölçüde azalır ve genlik daha yüksektir.
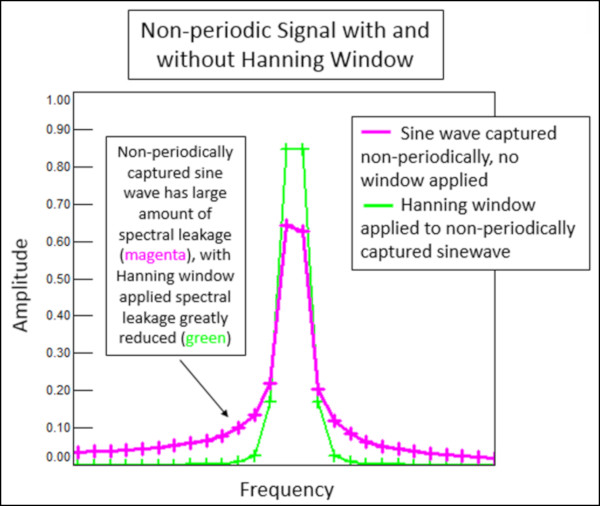
Maksimum genlik hatası, periyodik olmayan bir sinüs dalgasının spektrumunu görüntülerken görülebilir.
Frekans tepe noktası çevresinde bir RMS hesaplaması kullanılması, Şekil 8’de gösterildiği gibi bir pencere uygulandığında doğru değeri verir.Sinüs genliği 1 olan sinüs dalgasının RMS değeri 0.707 genliktir.
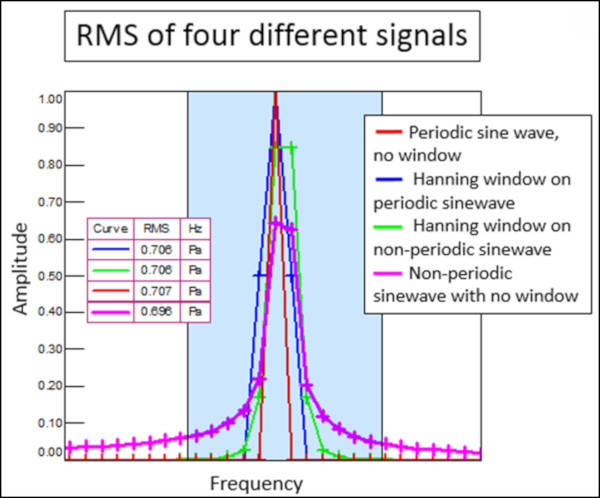
RMS hesaplaması, frekans aralığındaki enerjiyi toplar. Şekil 8’de, Hanning pencereli periyodik ve periyodik olmayan sinyallerin RMS değeri, sızıntısız sinüs dalgasının RMS değerine eşittir. Sadece bir pencere uygulanmayan periyodik olmayan sinüs dalgasının RMS değeri diğerlerine eşit değildir.
Flattop
Flattop penceresi Hanning penceresine kıyasla frekans alanında daha iyi bir genlik doğruluğuna sahiptir (Şekil 9). Flattop penceresinin maksimum genlik hatası%0.01’den azdır. Aksine, Hanning penceresinin maksimum genlik hatası%15’tir.
Bu maksimum genlik hataları, genlik düzeltme faktörlerinin frekans spektrumlarına uygulandığını varsayar. Bu genlik düzeltme faktörleri, bir pencere uygulanmasının neden olduğu genlik azalmasını telafi eder.
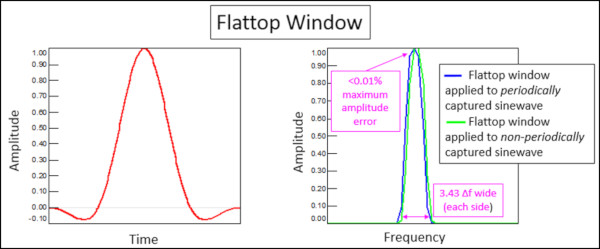
Bir Flattop penceresi, sızıntıyı orijinal sinyalin her bir tarafından 3,43 spektral çizgiyle sınırlar. Bu, Hanning penceresinin 1,5 spektral çizgi genişliğinden daha geniş bir frekans aralığına denk gelmektedir.
Bir Hanning penceresi gibi, Flattop penceresi de sıfır değeriyle başlar ve biter. Pencerenin merkezi 1 değerine sahiptir (Şekil 10).
Flattop penceresinin frekans doğruluğu, Hanning penceresine kıyasla daha kabadır. Sonuç olarak, Flattop penceresi tipik olarak frekans tepelerinin farklı ve birbirinden iyi ayrıldığı verilerde kullanılır. Frekans tepelerinin iyi ayrılması garanti edilmediğinde, Hanning penceresi tercih edilir çünkü spektrumda bireysel tepelerin kaybolmasına neden olma olasılığı daha azdır (Şekil 11).
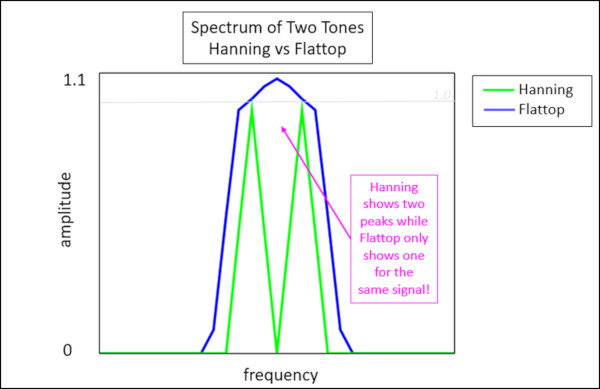
Şekil 11’de, periyodik olarak yakalanan iki tonun spektrumu gösterilmektedir. Tonlar 4 Hertz aralıklıdır ve 1 Hertz frekans çözünürlüğüyle yakalanmıştır. Yeşil eğri bir Hanning penceresine sahiptir ve doğru genlikte iki farklı ton gösterir. Mavi eğriye bir Flattop penceresi uygulanır ve yalnızca bir ton gösterdiği görülür. Bunun nedeni, Flattop penceresinin Hanning penceresinden daha fazla miktarda frekans etki alanında sızıntı oluşturmasıdır. Tonların orijinal frekanslarında genliğin doğru ve her iki pencere için bire eşit olduğunu unutmayın.
Flattop penceresi için yaygın olarak kullanılan bir uygulama kalibrasyon işlemidir. Örneğin, sağlam bir mikrofon kalibratörü, mikrofon kalibrasyonu sırasında yalnızca tek ve belirgin bir frekans üretir. Simcenter Testlab‘ın (eski adıyla LMS Test.Lab) ‘AC Calibration’ çalışma sayfasında, ‘Measurementinfo’butonuna basmak, Şekil 12’de gösterildiği gibi bir Flattop penceresinin kullanıldığını gösterir.
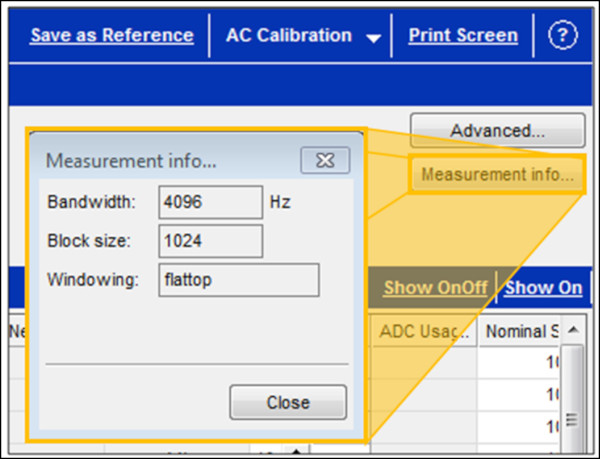
Genlik doğruluğunu sağlamak için, kalibrasyon penceresi tipi kullanıcı tarafından değiştirilemez. Ölçüm için farklı bir pencere seçilse bile, her zaman bir Flattop kullanılacaktır.
Uniform
Uniform penceresi, Şekil 13’te gösterildiği gibi tüm ölçüm süresi boyunca 1 değerine sahiptir. Gerçekte, Uniform Pencere ‘Pencere yok’ olarak adlandırılabilir. Kullanılan veri toplama sistemine bağlı olarak, bazen “Rectangular” penceresi olarakta kullanılır.
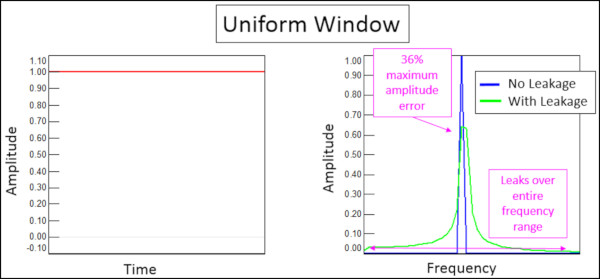
Uniform pencere, ölçülen sinyal periyodik olduğunda hiçbir frekans veya genlik bozulması oluşturmaz.
Ölçülen bir sinyal periyodik olmadığında, genlik maksimum%36 oranında azaltılır ve frekans içeriği ölçümün tüm bant genişliği boyunca yayılır. Bu, ölçülen sinyalin tekrarlanması ve eklenmesi ile oluşturulan keskin geçici nedenlerden kaynaklanır.
Bir ölçüm sinyali periyodik olduğunda, Uniform bir pencere tercih edilir. Periyodik bir sinyale bir Hanning veya Flattop penceresi uygulamak genlik ve frekans bozulması yaratacaktır.
Periyodik sinyaller şunları içerebilir:
– Ölçüm süresi boyunca sıfırdan başlayan ve biten ‘BurstRandom’ bir sinyal
– Ölçüm süresi ile tamsayı ilişkisi olan sinüzoidal sinyaller
– Ölçüm süresi içinde tamamen sıfırlanan darbe ölçümleri
Tukey
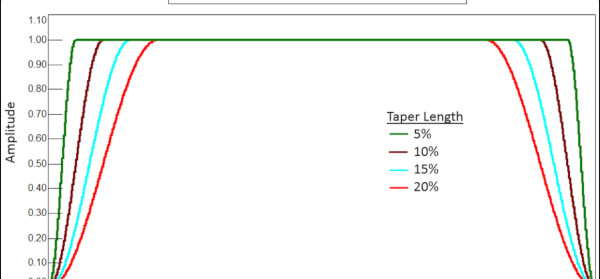
Bir Tukey penceresi zaman alanında çok düzdür, pencerenin çoğunluğu için 1 değerine yakındır. ‘’TaperLength’’ veri toplama süresinde pencerenin ne kadar 1 değerine sahip olacağını belirler. (Şekil 14). TaperLenght ne kadar düşük olursa, Tukey penceresinin ölçüm süresi boyunca 1 değeri o kadar uzun olur.
Tipik olarak, geçici verileri analiz etmek için Tukey pencereleri kullanılır. Bir Tukey penceresinin avantajı, zaman alanındaki geçici sinyalin genliğinin Hanning veya Flattop kullanımına kıyasla daha az değişme olasılığıdır (Şekil 15). Bir Hanning veya Flattop penceresinde, pencerenin değeri Tukey penceresine kıyasla daha kısa bir aralık için 1’e eşittir.
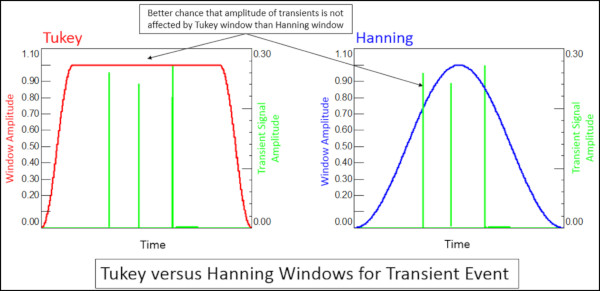
Tipik etki olayları birkaç milisaniye sürebilir. Örnekler arasında çekiçlerden kaynaklanan titreşimler, yoldaki tümsekler veya dizel motor tıkanıklığı sayılabilir.
Exponential
Exponential pencereler genellikle modal darbe testinde kullanılır. Sızıntı sorunlarını önlemek için ivmeölçer yanıtının ölçüm süresi içinde sıfıra (Şekil 16) düşmesini sağlamak için kullanılırlar.
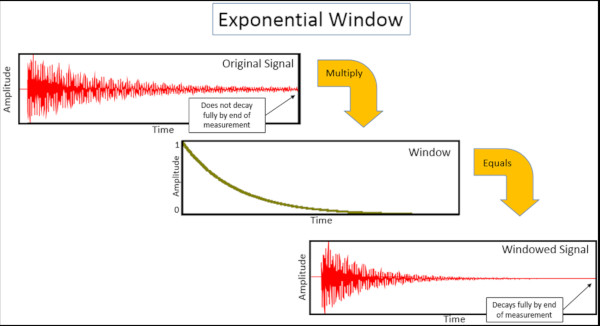
Exponential bir pencere her zaman ölçümün başında 1.0 değeri ile başlar.
Exponentialbozunma parametresi,%0 ile%100 arasında bir değer olup, Exponential pencerenin başlangıç değerinin, ölçümün sonuna kadar ne kadar azaltılacağını belirler. Örneğin,%25’lik bir bozunma parametresi, Şekil 17’de gösterildiği gibi, ölçüm tamamlandığında pencerenin orijinal genliğin dörtte birine düştüğü anlamına gelir.
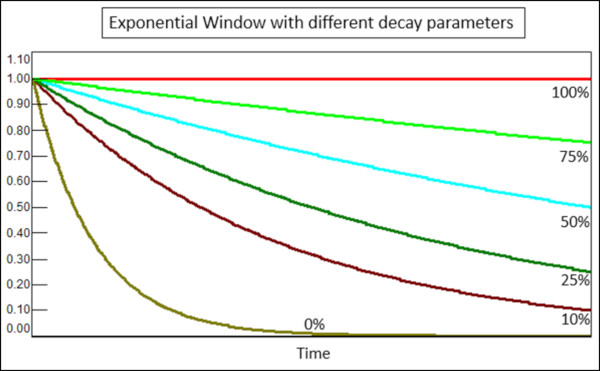
%100’lük bir Exponentialbozunma parametresi, Uniform bir pencereyle aynıdır (veya bir pencere uygulamaz). Model darbe testi yaparken, ölçüm zaman aralığında sinyal sıfıra düşerse%100’lük bir bozunma tercih edilir.
Exponential bir pencere uygulandığında, ölçülen sinyal orijinal sinyalden daha hızlı bozulur (Şekil 18).
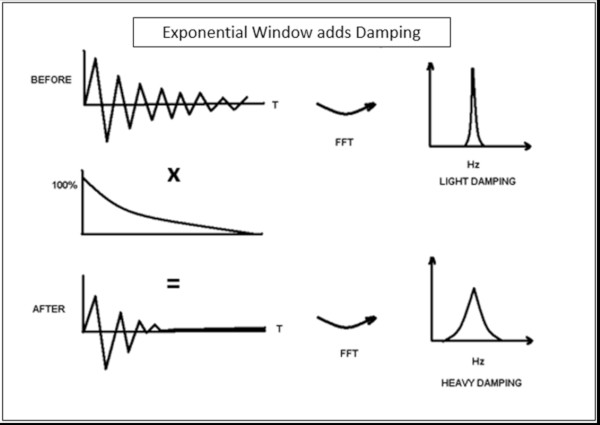
Daha hızlı bozunmayla, ortaya çıkan ölçüme yapay sönümleme eklenir. Verilere kaydedilen Exponentialbozunma parametresini kullanarak, SimcenterTestlab’dakimodsal eğri oluşturucular efektleri kaldırabilir ve doğru mod sönümleme değerlerini rapor edebilir.
Sonuç
Ölçüm verisi koşullarına uygun bir pencere seçmek, doğru ve kullanışlı veriler elde etmek için önemlidir. Örneğin, Flattop penceresi bir kalibrasyon gerçekleştirmek için idealdir, ancak Exponential bir pencere uygun değildir.
Umarım bu makale hangi pencerelerin ve hangi koşullar altında kullanılacağı konusunda faydalı rehberlik sağlar.
Uygulama hakkında sorularınız için DTA Mühendislik Test Bölümü mühendisleriyle iletişime geçebilirsiniz.



Bu makale için ne kadar teşekkür etsem az. Elinize sağlık.