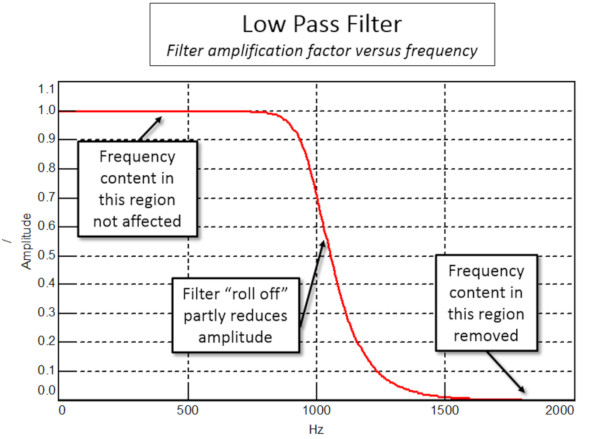
Filtrelerin veri toplama ve analizinde çeşitli uygulamaları vardır. Belirli frekansları azaltarak veya artırarak bir zaman sinyalinin frekans içeriğini değiştirmek için kullanılırlar.
Örneğin, Şekil l’de gösterildiği gibi, bir Alçak geçiren (Low Pass) filtresi, bir sinyaldeki frekans içeriğini üç farklı şekilde etkiler: Bazı frekans içeriği değişmeden kalır, diğer frekans içeriği ise genlik olarak azaltılır veya tamamen sinyalden çıkarılır.
Filtreler ayrıca, sadece azaltmak veya kaldırmak değil, frekans içeriğini de yükseltebilir. Bir filtrenin, bir sinyalin genliğini ayarladığı miktar, Şekil 2’de gösterildiği gibi ya doğrusal terimlerle (yani güçlendirme faktörü) ya da desibel arttırma / azaltma ile ifade edilebilir.
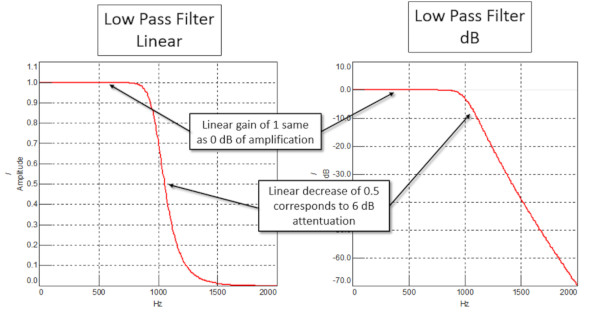
Doğrusal ölçek desibel ölçeğinde aşağıdaki eşdeğerlere sahiptir:
– Doğrusal genliğin yarıya indirilmesi, 6dB azaltmaya eş değerdir.
– Doğrusal genliğin 1 veyaazaltma değeri 0 dB olduğunda, genlik değişmez.
Filtre karakteristiğini frekans alanında görüntülemek daha kullanışlı olsa da filtreleme işlemi zaman alanına uygulanır.
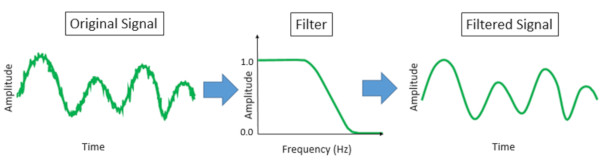
Filtre, zaman alanındaki sinyali giriş olarak alır, frekans içeriğini değiştirir ve zaman alanında yeni bir sinyal verir. Filtreleme, çeşitli uygulamalar için kullanışlı olabilir.
Makale içerikleri;
1. Filtre Uygulamaları
2. Filtre Çeşitleri
3. FIR ve IIR
4. Filtre Mertebesi ve Hesaplama Hızı
5. Zaman Gecikmesi ve Filtreler
6. Filtre Metotları ve Özellikleri
6.1. FIR Filtre Metotları
6.2. IIR Metotları
7. Simcenter Testlab Filtreleme
1.Filtre Uygulamaları
Filtreler, sinyal temizlemeden analize kadar farklı şekillerde kullanılır.
Bazı uygulamalarda, filtreler, istenmeyen frekans içeriğini azaltarak bir zaman alanı sinyalini koşullandırmak için kullanılır. Örnekler:
– Anti- aliasing filtresi- Analogdan dijitale dönüşümden önce düzgün şekilde dijitalleştirilemeyen sinyal içeriğini kaldırmak için anti-aliasing filtresi kullanılır.
– Gürültü Giderme- Filtreler, bir sinyalden istenmeyen yüksek frekanslı gürültüyü gidermek için kullanılabilir. Örneğin, bir müzik kaydındaki tıslama gibi.
– Sapma Giderme- Sapma ya da büyük ofsetler yüksek geçiren filtre ya da AC coupling ile sinyalden giderilebilir.
Bazen, filtreler analiz için belirli karakteristiği sinyal verisine eklemek için kullanılır:
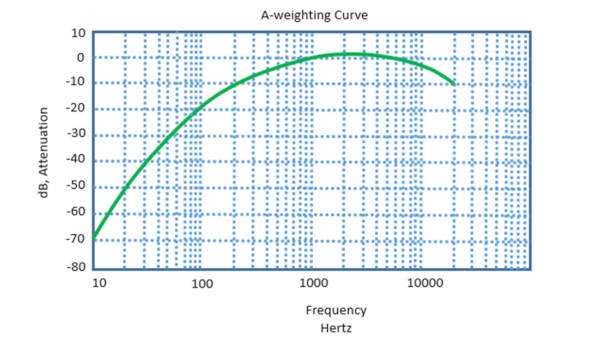
– A- Weighting- A weighting filtresi insan duyma karakteristiğini mikrofon verisine eklemekte kullanılır. Bir mikrofon bütün frekansları eşit şekilde “duyar”, ama insan kulağı duymaz. A- weighting filtresi mikrofon sinyalindeki yüksek ve düşük frekansları azaltır ve insan kulağı açısından nasıl algılandığını yansıtır.
– Bütün Vücut Titreşim Ağırlıklandırması (Whole Body Vibration Weighting): İnsan vücudu belirli titreşim frekanslarına diğerlerinden daha duyarlıdır. Bir ivmeölçer titreşim sinyaline dayalı olarak insan vücudu sağlığını ve konforunu değerlendirmek için bir filtre (ISO 2631 ile tanımlanmıştır) kullanılabilir.
Filtreler analog (sürekli sinyaller için) sistemlerde veya dijital olarak (önceden kaydedilmiş bir sinyalin PC’de manipülasyonu için) uygulanabilir.
2. Filtre Çeşitleri
Filtreler çeşitli amaçlar için tasarlanabilir. Örneğin, bir filtre yüksek geçiren, alçak geçiren, bant durduran veya bant geçiren olarak sınıflandırılabilir. (Şekil5)
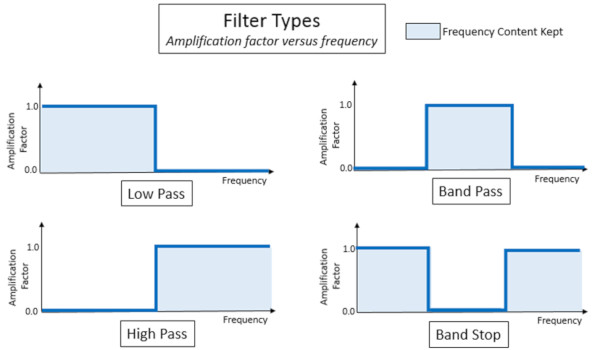
Filtre Çeşitleri:
– Yüksek geçiren– Yüksek geçiren filtre düşük frekanslardaki ofsetleri gidermek için kullanılır. Örneğin, eğer bir gerinim pulu sinyalindeki dinamik içerik ile ilgileniliyorsa, yüksek geçiren filtre kullanılarak düşük frekanstaki sapmalar giderilebilir.
– Alçak geçiren – Belirli bir frekansın üzerinde kalan frekansları zayıflatır, kaldırır. Örneğin, ses kaydında yüksek frekanslarda bulunan cızırtıları gidermek için kullanılabilir.
– Bant geçiren – Bu filtre, frekans içeriğinin sadece bant sınırlı bir kısmının filtreden geçirilmesine izin vermek için kullanılır.
– Bant durduran – Belirli aralıkta bulunan frekans içeriğini silmek için kullanılır.
Filtre çeşitleri, FIR veya IIR filtreleri olarak da ayrıştırılabilir. Keyfi şekilli bir filtre üretmek için bunların bir kombinasyonunu kullanmak da mümkündür.
3. FIR ve IIR
Dijital filtrelerin iki çeşidi vardır. Bunlar Finite Impulse Response (FIR) ve Infinite Impulse Response (IIR).
“Impulse Response” terimi, filtrenin zaman alanındaki görünümünü belirtir. Filtreler tipik olarak, Şekil 6’da gösterildiği gibi zaman alanındaki kısa süreli darbelere karşılık gelen geniş frekans tepkilerine sahiptir.
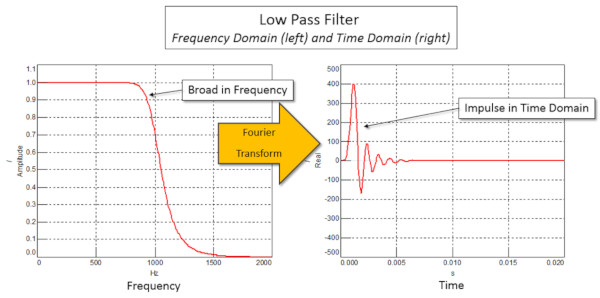
Hem IIR hem de FIR filtresi için denklemler Denklem 1’de gösterilmiştir. Filtreye giriş zaman serisi x (n) ve filtrenin çıkışı bir zaman serisi y (n). Zaman sinyalindeki ilk örnek n = 0’dır.

IIR ve FIR uygulaması arasındaki matematiksel fark, IIR filtresinin filtre çıkışının bir kısmını girdi olarak kullanmasıdır. Bu, IIR filtresini “recursive” (özyinelemeli) bir işlev haline getirir.
Her denklemin üç sayı serisi vardır: bir giriş zaman sinyali, bir filtre ve bir çıkış zaman sinyali (Şekil 7).
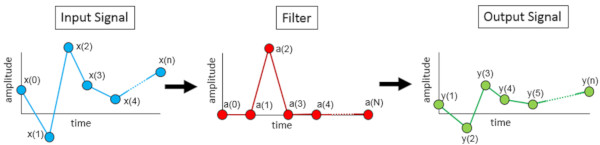
Bu seriler:
– X(n) – Zamanda giriş serisi, x (0), x (1), x (2), x(n)’ e kadar. “n” sayısı zaman alanındaki giriş sinyalinin veri noktalarının toplam sayısıdır.
– A(k) – Filtre “a” olarak isimlendirilen seriyle, FIR filtre olarak tanımlanmaktadır, IIR filtre için “a” ve “b” etiketli serilerle ifade edilir.” N” ve “P” sırasıyla “mertebe” ve “bağlantı sayısı” olarak da adlandırılan, filtrelerdeki terim sayılarıdır. Örneğin, FIR filtresi k=0 ila k=N arasında gerçekleştirilir.
– Y(n) – Çıkış zaman sinyali, y (0), y (1), y (2), ….
Uygulamada, FIR ve IIR filtreler önemli performans farklılıklarına sahiptir, Şekil 8’ de özet halinde mevcuttur.

IIR filtresinin, FIR’a benzer bir filtre dönüşümü için daha düşük bir mertebe veya terim sayısının kullanılabilir. Yani, aynı sonucu elde etmek için daha az hesaplama yapılması gerekir ve bu da IIR filtresinin daha hızlı hesaplama yaptığını gösterir. Bununla birlikte, IIR filtresinin doğrusal olmayan faz ve stabillik sorunları vardır. Biraz kaplumbağa ve tavşanın masalı gibi. FIR filtresi yarıştaki kaplumbağa gibidir- yavaş ve sabittir ve daima biter. Tavşan IIR filtresi gibidir- çok hızlı, ancak bazen tökezler ve yarışı tamamlayamaz.
Bu farklılıklar sonraki bölümlerde daha ayrıntılı olarak ele alınacaktır.
4. Filtre Mertebesi ve Hesaplama Hızı
FIR filtre denkleminde, N sayısı, filtrenin mertebesini belirtir. Örneğin 5 elemanlı ve 10 elemanlı filtreleri karşılaştırdığımızda, filtre hesaplanması iki kat uzunlukta olacaktır. Fakat, filtre Şekil 9’da görüldüğü gibi daha keskin olacaktır.
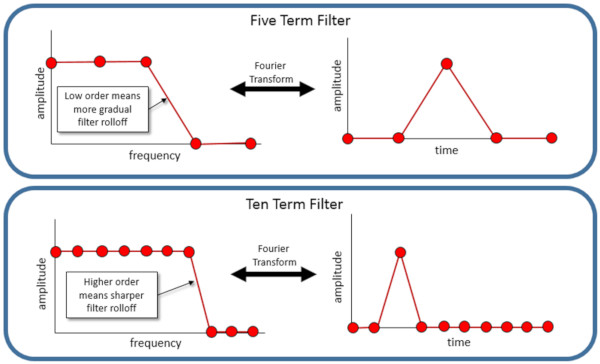
Daha fazla terime sahip bir filtrenin (yani, daha yüksek bir mertebe) geçirilen frekanslar ile durdurulan frekanslar arasında daha keskin bir geçiş vardır.
Farklı filtre mertebeleriyle hesaplanan aynı filtre tipinin örnek karşılaştırması, Şekil 10’da gösterilmektedir.
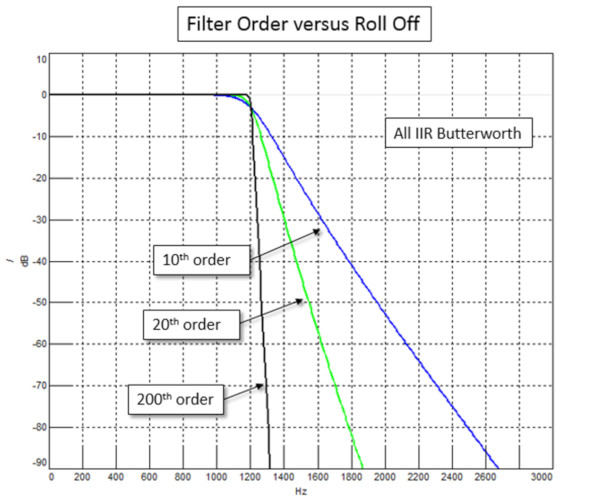
Mertebeyi arttırmak, filtreyi daha keskin hale getirir. Bu daha fazla hesaplama gerektirir ve filtre tarafından kaynaklanan zamanda gecikmeye neden olur.

FIR ve IIR filtrelerin keskinliği, Şekil 11’de gösterildiği gibi aynı mertebeye göre çok farklıdır. Filtre çıkışının bir kısmının girdi olarak kullanıldığı IIR filtresinin recursive yapısı (bkz. Denklem 1) nedeniyle daha keskin bir sonuç elde edilir, aynı mertebe ile daha keskin düşüşü başarır.
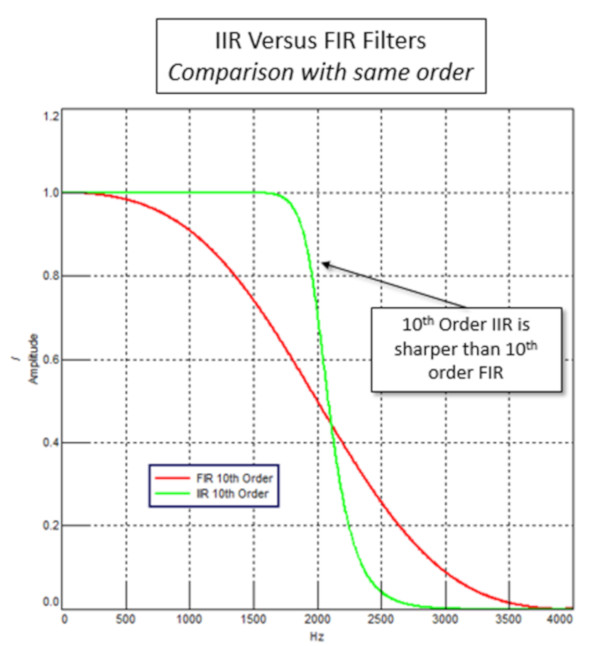
Bununla birlikte, Şekil 12’de gösterildiği gibi bir FIR ile aynı performansı elde etmek için bir IIR’de daha az terim kullanılabilir.
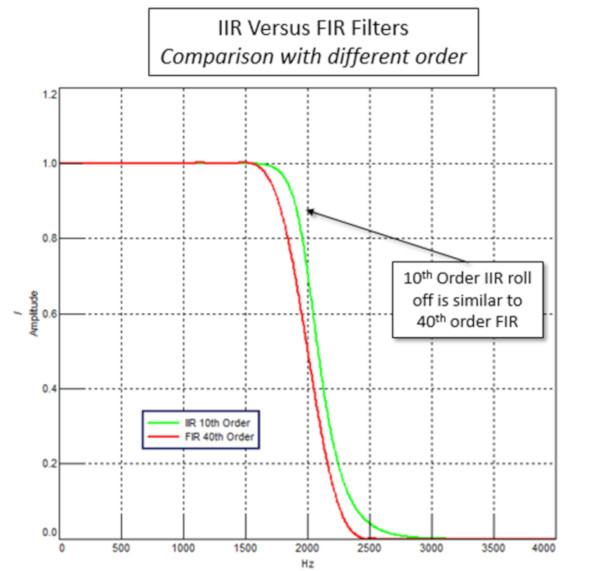
Bu durum, IIR filtrelerini hesaplama açısından FIR filtrelerinden daha hızlı hale getirir. Bir filtrenin gerçek zamanlı uygulamada kullanılması gerekiyorsa (örneğin dinlerken interaktif filtreleme), tipik bir IIR filtresi ile yapılır.
Bununla birlikte, bir IIR filtresi kullanmanın bazı dezavantajları vardır:
– Gecikmeler- Bir IIR filtresinin farklı frekanslarda eşit olmayan bir gecikmesi varken, FIR filtresi her frekansta tutarlı bir gecikmeye sahiptir.
– Kararlılık- Yapısından dolayı, bir IIR filtresi bazen kararsız olabilir ve veri hesaplanamaz veya verilere uygulanamaz. FIR filtre denklemi her zaman kararlıdır.

5. Zaman Gecikmesi ve Filtreler
Zaman verilerine bir filtre uygulandığında ve orijinal zaman verisi ile karşılaştırıldığında, verilerde hafif bir kayma veya zaman gecikmesi görülebilir. Şekil 13’te, aynı anda elde edilen ses (kırmızı eğri, üst) ve titreşim verileri (mavi eğri, alt) gösterilmiştir. Ses verilerinin filtrelenmesi (yeşil eğri, üst) ses ve titreşim arasındaki olayların hizalanmamasına neden olur.
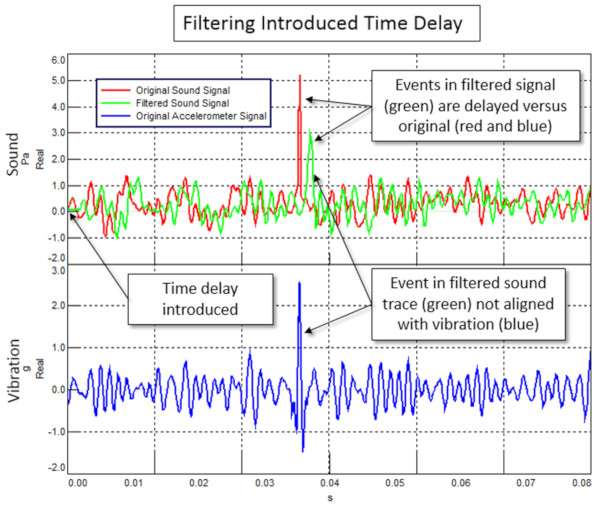
Bazı uygulamalarda bu bir sorun teşkil etmez- ofset bilinir ve göz ardı edilebilir.
Diğer bazı uygulamalarda, bu gecikme önemli olabilir.
Örneğin:
– Troubleshooting(Sorun Giderme) – Çok kanallı ses ve titreşim kaydı ile, yalnızca ses kanalına bir filtre uygulanırsa, ses kanalına titreşim kanallarına göre bir zaman gecikmesi eklenir (Şekil 13’teki alt grafiğe bakın). Bir titreşim olayının ses oluşturup oluşturmadığını anlamaya çalışırken, buradaki yanlış hizalama titreşim ve ses olaylarının ilişkili olup olmadığını görmeyi zorlaştıracaktır.
– Operational Deflection Shapes (ODS) – ODS de kullanılan bazı titreşim kanallarına filtre uygulanmış ve diğerlerine uygulanmamışsa, bu kanallar arasındaki faz ilişkisinin değişmesine neden olur. Sonuç olarak, animasyon doğru olmaz.
Filtrelerin, zaman alanında çıkış sinyallerinde zaman gecikmesi getirmesine ne sebep olur?
Şekil 14’teki bir FIR filtresi için denklemi alın. Denklem ile çalışırken, zaman gecikmesinin nedeni gözlenebilir.
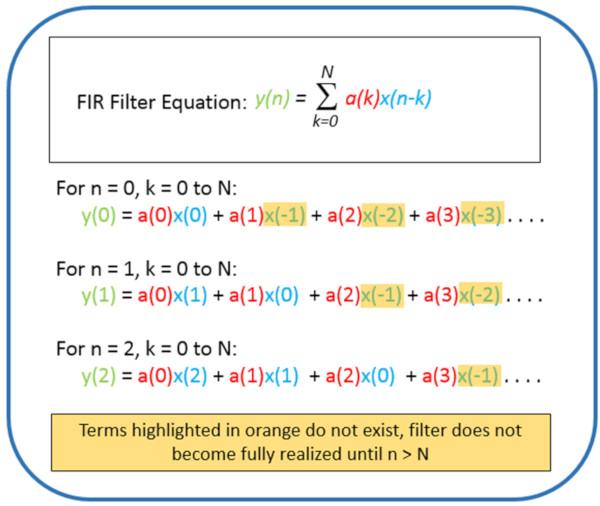
Filtre çalışmadan önce, giriş sinyalinden (x) gelen birkaç zaman veri örneği, terimlerin sayısıyla (N) orantılı olan filtreden geçmelidir. Filtrelenen çıkış verileri, filtreden geçen (n) veri noktası N’den büyük olana kadar başlamaz.
Bazı verilerin bir çıktı oluşturmak için bile filtreden geçmesi gerektiğinden, Şekil 13’te gösterildiği gibi, giriş zaman sinyaline (x) kıyasla çıkış zaman sinyalinde (y) bir gecikme yaratılır.Filtreyi daha keskin hale getirmek, gecikmeyi artırır.

IIR ve FIR filtrelerinin gecikme karakteristikleri, Şekil 15’te gösterildiği gibi çok farklıdır.
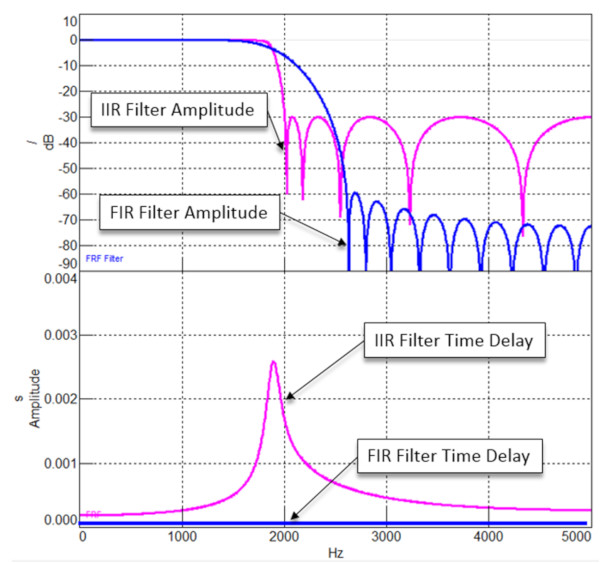
FIR filtresinin tüm frekanslarda eşit zaman gecikmesi olurken, IIR filtre zaman gecikmesi frekansa göre değişir. Genellikle IIR filtresindeki en büyük zaman gecikmesi filtrenin kesme frekansındadır.

Tüm filtreler bir tür analog ve dijital gecikme oluşturur. Filtre özelliklerine bağlı olarak, gecikme daha kısa veya daha uzun olabilir. Ayrıca frekansın bir fonksiyonu olarak değişken olabilirler.
Direct ve Zero Faz
Çıktı zaman sinyalindeki gecikme, verileri ‘ileri ve geri’ filtreleyerek ortadan kaldırılabilir. Zaman sinyali x (n) filtrelendikten ve yeni çıkış zamanı sinyali y (n) oluşturulduktan sonra, filtreye geri beslenebilir. Bunu yapmak için y (n) ‘deki veri noktaları zaman içinde ters çevrilir ve tekrar filtreye beslenir. Buna “sıfır faz filtreleme” denir. Sonuç Şekil 16’da gösterilmektedir.
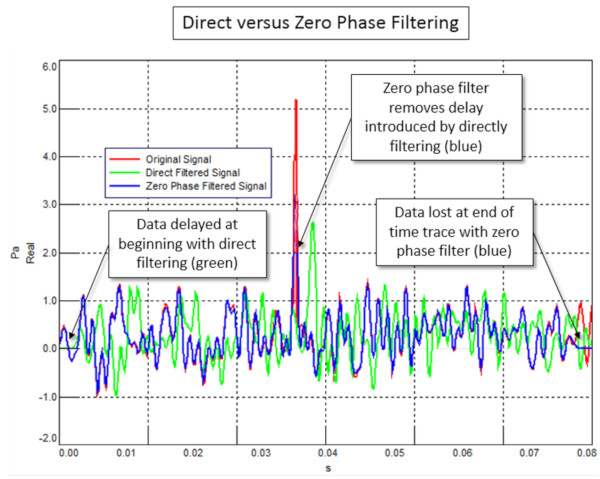
“Sıfır faz” filtre sadece y (n) çıkışı x (n) ile hizalanmakla kalmaz, veriler iki kez filtrelenir, böylece zayıflama iki katına çıkar. Sıfır fazlı filtreler kullanılırken bazı ödünler verilir:
– Hesaplama iki kat uzun sürede gerçekleşir.
– Sadece dijital sinyallerle kolayca yapılır, analog sinyallerle kolayca yapılmaz.
– Zaman ekseninin sonundaki veriler yok olur.

6. Filtre Metotları ve Özellikleri
Filtre katsayıları, a(n), belirli filtre niteliklerini kontrol etmek için seçilebilir. Katsayılar veya yöntemler, Şekil 17’de gösterilen filtre niteliklerini etkiler.
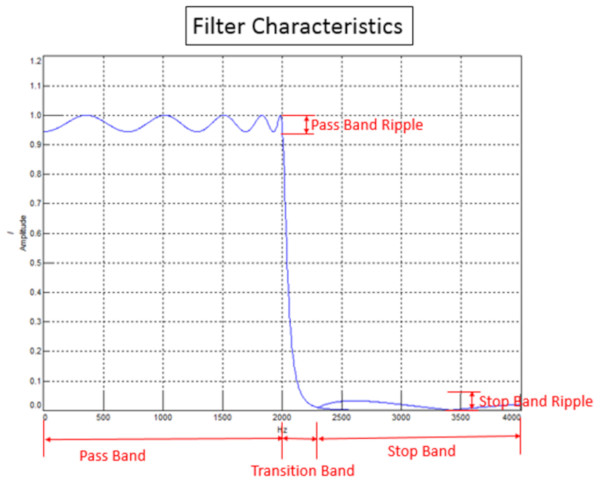
Yöntemlerin etkilediği dört ana filtre özelliği vardır:
– Geçirme Bandı- Geçirme bandındaki veriler doğrudan çıkış zaman sinyaline gönderilir. Geçirme bandındaki verilerin orijinal zaman sinyalleri ile aynı olduğundan emin olmak için filtrede herhangi bir dalgalanma olmamalıdır. Dalgalanma, frekansın fonksiyonu olarak genlikte küçük bir değişikliğe neden olur. İdeal olarak, bu bantta filtrenin tam olarak bir genliği olmalıdır.
– Geçiş Genişliği- Uygulamaya bağlı olarak, geçirme ve durdurma bantları arasındaki geçiş genişliğinin frekans açısından mümkün olduğunca dar olması arzu edilebilir. Hem yöntem hem de filtre mertebesi, geçirme ve durdurma bantları arasındaki geçiş bandının ne kadar hızlı gerçekleştiğini belirler.
– Durdurma Bandı- Filtrenin dalgalanması varsa durdurma bandı da veri içerebilir. Bazı uygulamalarda, genlik önemli olmadığı kadar küçük olabilir. Diğerlerinde ise, dalgalanma kabul edilemeyebilir.
– Grup Gecikmesi/Faz- Filtreler çıkış zaman sinyalinde bir gecikme oluşturur ve bu, frekansın bir fonksiyonu olarak bile değişebilir. Daha önce açıklandığı gibi, bir filtreden ileri ve geri bir zaman sinyali çalıştırmak bu gecikmeyi kaldırır (Sıfır Faz filtresi). Fazın kritik olduğu ve sıfır fazlı filtre işleminin bir seçenek olmadığı bazı uygulamalar için bu dikkate alınması gereken önemli bir husustur.
6.1. FIR Filtre Metotları
Finite Impuls Response (FIR) filtre metotları aşağıda listelen, Şekil 18’ de gösterilmiştir.
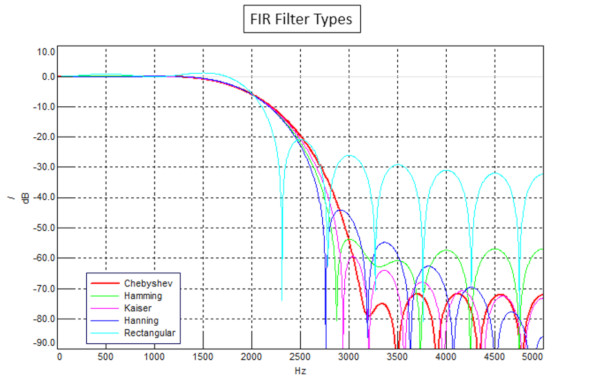
FIR yöntemleri, frekanstan zaman alanına dönüşüm yaparken farklı spektral pencereler kullanır. Bazı pencere yöntemleri şunları içerir:
– Chebyshev- Durdurma bandında en düşük dalgalanma miktarına sahiptir, ancak en geniş geçiş bandına sahiptir.
– Hamming- Dar geçiş bölgesi, Hanning’den daha küçük dalgalanma. Manhattan Projesinin bir üyesi olan Richard Hamming tarafından geliştirildi.
– Kaiser- Bell Laboratuarlarında James Kaiser tarafından geliştirilen Kaiser penceresinde durma bölgesinde küçük genlik dalgalanması var, sadece geniş geçiş genişliği Chebyshev daha düşük genlik dalgalanmasına sahip.
– Hanning- En dar geçiş bandı, ancak durdurma bandında büyük dalgalanma.
– Rectangular- En büyük dalgalanma / lob miktarı, geçirme bandını bile etkiler.
6.2. IIR Metotları
Infinite Impulse Response (IIR) metotları, Şekil 19’da gösterilmiştir.
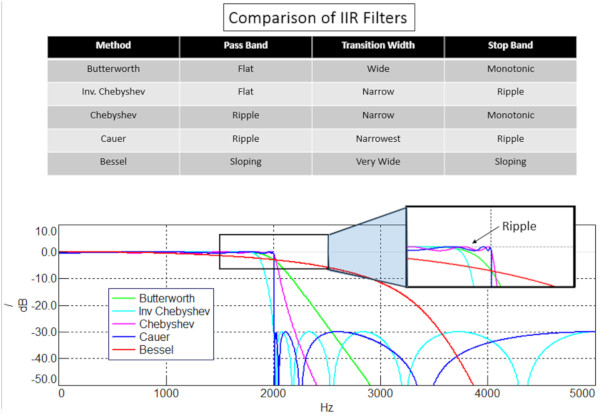
Farklı IIR filtre metotlarının özellikleri:
– Butterworth- Hem geçirme hem de durdurma bandında düz tepki, ancak geniş bir geçiş bölgesine sahiptir. İlk olarak 1930’da İngiliz fizikçi Stephen Butterworth tarafından tanımlandı.
– Inverse Chebyshev- Geçirme bandında düz, Butterworth filtresinden daha dar bir geçiş genişliğine sahip, ancak durdurma bandında dalgalanma var. Durdurma bandındaki dalgalanma bir sorun değilse, belirli bir uygulama için Butterworth filtresine karşı tercih edilebilir.
– Chebyshev- Geçirme bandında dalgalanma olabilir, ancak Ters Chebyshev’den daha dik bir düşüş vardır.
– Cauer- En dar geçiş bölgesi. Hem durdurma hem de geçirme bantlarında dalgalanma. Bazen Eliptik filtre denir.
– Bessel- Çok geniş bir geçiş bölgesi ile hem geçirme hem de durdurma bandında eğimli genlik. Filtredeki gecikmeye karşı frekans bu listedeki en düzdür. Bessel filtresi, Alman bir matematikçi olan Freidrich Bessel (1784-1846) için seçildi.

Belirli bir uygulamaya en uygun filtre yöntemi seçilebilir.
7. Simcenter Testlab / Filtreleme
Simcenter Testlab‘de filtreler, “Time Data Selection” çalışma sayfasındaki “Time Signal Calculator” (Tools>Add-ins>Time Signal Calculator, 26 tokens) kullanılarak kaydedilen sinyallere uygulanabilir.
Time Signal Calculator’ın filtreleme özellikleri Koşullandırma (Conditioning) grubundadır. Bir Alçak geçiren filtresi (Low pass filter) eklemek için, fonksiyon Şekil 20’de gösterildiği gibi “FILTER_LP” olarak adlandırılır.
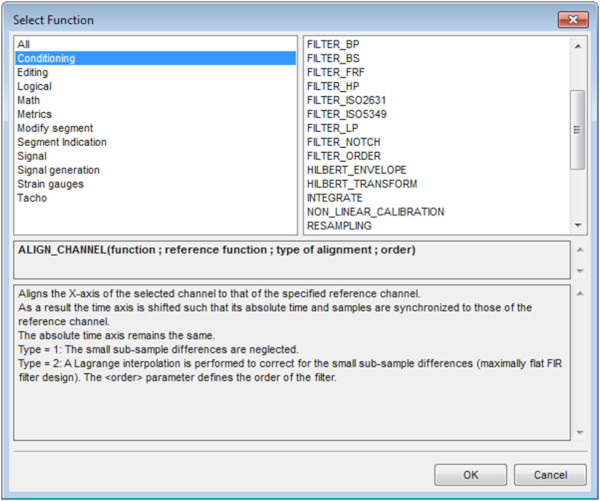
Fonksiyon eklenirken, filtre tipi (IIR ve FIR), mertebe, metot vb. Şekil 21’de gösterildiği gibi belirtilebilir.
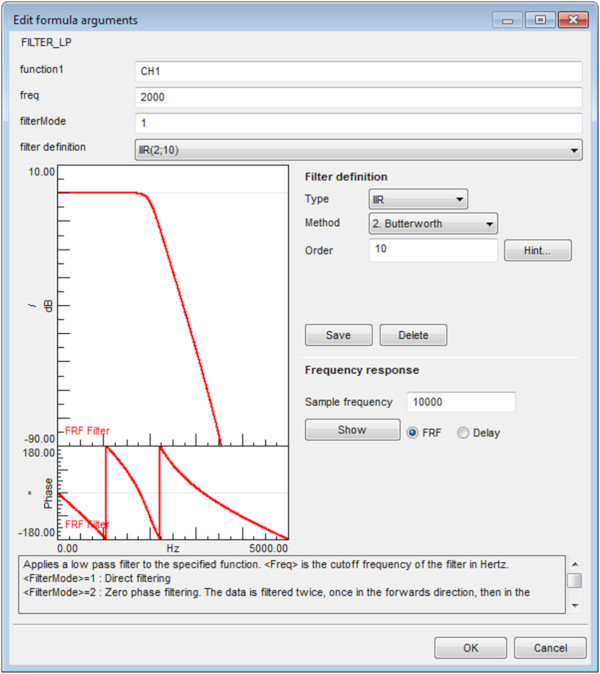
“Örnekleme Frekans (Sample frequency)” seçiminin filtre performansı veya özellikleri üzerinde hiçbir etkisi yoktur. Filtre şeklinin görselleştirileceği frekans aralığını tanımlamak içindir.
“Show” butonu filtre şeklini, fazı ve grup gecikmesini görselleştirmek için kullanılabilir.
Uygulama hakkında sorularınız için DTA Mühendislik Test Bölümü mühendisleriyle iletişime geçebilirsiniz.