Rozet Tipi Gerinim Pulları
Tek dirence sahip bir gerinim pulu sadece bir yöndeki gerinimi ölçebilir. Bu durum gerçek hayattaki uygulamalarda, karmaşık yüklemeleri içeren yapılar için yetersiz kalmaktadır.
Gerilmeler farklı yönlerde oluşabilir, bu nedenle ölçüm yöntemimiz birkaç farklı yöndeki gerinimi aynı anda ölçebilecek yetenekte olmalıdır.
Tek dirençli gerinim pullarının yük çeşitlerine göre kıyaslanması
Aşağıdaki gerinim pulunun farklı yüklemelerdeki ölçüm doğruluklarını kıyaslayalım;
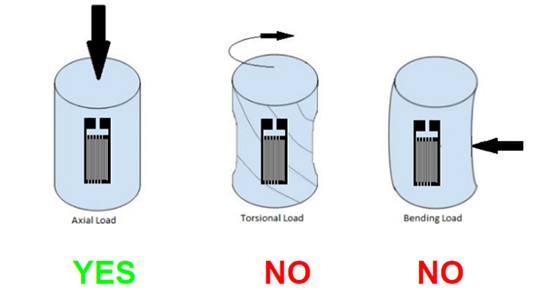
Metal bir silindire uygulanan farklı tipteki yükleme durumlarından gerinim ölçmek istediğimizde, sadece en soldaki gerinim pulu yapıdaki strain’i doğru ölçecektir. Diğerlerinde olduğu gibi burulma ve eğilme gibi durumlarda, yani farklı doğrultularda stress oluşturan yükleme durumlarında bu yöntem yanlış sonuçlar almamıza sebep olacaktır. Bu gibi durumlarda ise rozet tipi gerinim pulları ile ölçüm almamız gerekir.
Gerinimi tek tek eksenler halinde düşünmek yerine, aşağıda görüldüğü üzere XY ekseninde düzlemsel bir yaklaşım kullanarak ifade edebiliriz.
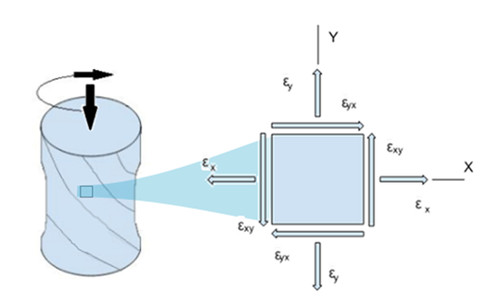
Gerinim, kendini bu düzlemde üç şekilde belli eder.
– X yönündeki normal gerinim (εx)
– Y yönündeki normal gerinim (εy)
– XY’deki kayma gerinimi (εxy)
Gerinim Tensörü ve Asal Gerinim
Gerinimi düzlemde tanımlamanın iki metodu vardır; gerinim tensörü ve asal gerinim. Her iki metot da parçanın aynı noktadaki gerinimini aynı düzlemde, fakat farklı perspektiflerde tanımlarlar.
1. Method: Gerinim Tensörü: Bu metot yukarıdaki görselde görüleceği üzere iki normal (εx,εy ) ve bir kayma (εxy) olmak üzere üç gerinim konponenti içerir.
2. Method: Asal Gerinim: Bu metotta iki asal gerinim ve bir açı vardır. Burada değerler, düzlemde iki asal gerinim komponenti kalana kadar, yani kayma gerinimi sıfır olana kadar sanal olarak döndürülür. Burada açı ise, XY düzleminde kaç derecelik bir döndürme yapıldığını gösterir.
Aşağıdaki şekil bu durumu anlamamıza yardımcı olacaktır.
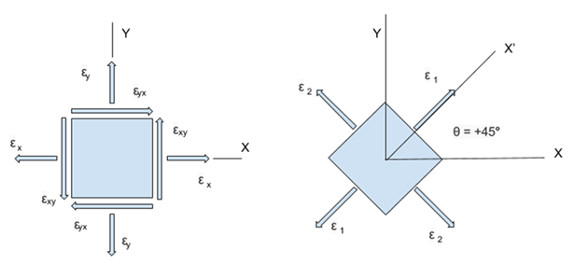
Asal gerinimlerin doğru tanımlanması çok önemlidir. Parçanın ömrü en büyük gerinime göre hesaplanır. Eğer bu değer elde edilemeyip daha küçük bir gerinim hesaba katılırsa, ömür tahmini yanlış sonuç verir ve parça hesaplanan ömürden daha kısa bir sürede bozunmaya uğrayabilir.
Gerinim tensörleri ile asal gerinimler arasındaki bağ, gerinim dönüşümü adında bir dizi eşitlik ile açıklanabilir. Gerinim dönüşümü, Mohr çemberi yardımıyla kolayca görselleştirilebilir (Şekil 4). Mohr çemberinde normal gerinim x ekseni ile, kayma gerinimi y ekseni ile temsil edilir ve bu model ile hem asal hem de maximum kayma gerinimini elde edebiliriz.
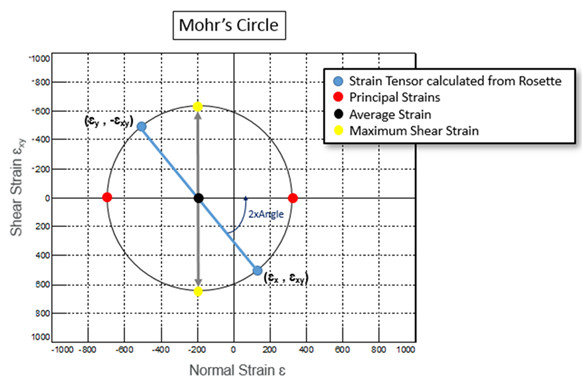
Mohr çemberinin özellikleri:
– İki normal (εx, εy) ve bir kayma (εxy) geriniminden oluşan gerinim tensörü, rozet gerinim pulundan ölçülen ε1, ε2, ε3 ‘den hesaplanır (Şekil 4, Şekil 5).
– Ortalama gerinim (εx+εy)/2 formülünden hesaplanır. Ortalama gerilme noktası ise bu çemberin merkezidir (Şekil 4, siyah nokta).
– Hesaplanmış normal ve kayma gerinimleri, grafikteki (εx,εxy) ve (εy,-εxy) noktaları (mavi) ile gösterilir. Bu iki noktanın arasındaki mesafe çemberin çapıdır.
– Çember üzerinde; kayma geriniminin sıfır hizasına denk gelen X ekseni üzerindeki noktalar(kırmızı), maximum ve minimum asal gerilmelerdir.
– Mohr çemberindeki açı rozet pulların açısının iki katıdır. Kullanılan çevrime bağlı olarak bu açı 0/180 veya -90/+90 arasında olacaktır.
– Mohr çemberinin aşağı doğru çizilen pozitif kesme gerilmesi ile yapıldığını unutmayın. Bu mohr çemberindeki açının pozitif dönme yönünün, rozet pullarının açısıyla aynı yönde olması için yapılır.
Genel olarak, CAE simülasyonlarının çıktısı gerinim metotu tabanlı normal ve kayma gerinimleridir. Rozet gerinim pulları kulllanılarak yapılan testlerin çıktıları ise asal gerinim tabanlıdır. Test ve CAE sonuçlarının karşılaştırılması için gerinim dönüşümü yapılmalıdır.
Rozet Gerinim Pulu Hesaplamaları
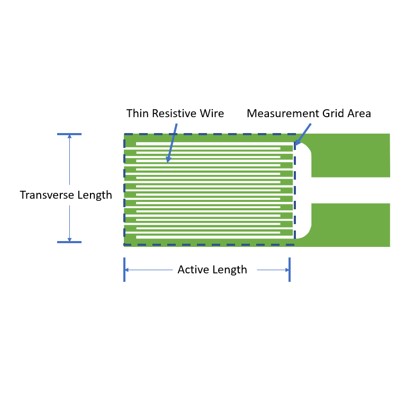
Rozet gerinim pulları çok yönlü gerinimleri ölçmek ve ölçülen bölgedeki bir noktanın asal gerilmelerini belirleyebilmek için kullanılır. Bu tip gerinim pulları, yüzeydeki normal gerilmeleri ölçmek için üç adet gerinim pulunun birbirleriyle belirli açılar yapacak şekilde bir araya getirilmesiyle elde edilir (Şekil 5).

Teorik olarak her gerinim pulu, yüzeyin aynı noktasındaki gerinimi ölçmelidir. Bu nedenle üç gerinim pulu rozet merkezine olabildiğince yakın yerleştirilirler. Eğer büyük gerinim gradyanları söz konusu ise, ölçümün tek noktadan olması şartına yakınlaşmak için pulların; yan yana yerine üst üste konumlandırıldığı ‘stacked’ tipi rozet gerinim pulları da kullanılabilir.
Rozet tipinin içerdiği üç gerinim pulundan alınan ölçüm, malzemenin young modülü ve poisson oranı; aşağıdaki dokuz değerin hesaplanmasında kullanılır.
– 1. Asal Gerinim (SN1) : 1. asal gerilme yönündeki gerinim
– 2. Asal Gerinim (SN2) : 2. asal gerilme yönündeki gerinim
– Kayma gerinimi (SNSH)
– Açı (AG) : 1. gerinim(ε1) ile asal eksen arasındaki açı
– 1. Asal Gerilme (SS1) : Maximum asal gerilme
– 2. Asal Gerilme (SS2) : Minimum asal gerilme
– Kayma Gerilmesi (SNSH)
– Eşdeğer Geilme (ES) : Von Mises’e göre eşdeğer gerilme
– Biaxiality Ratio (BR) : İki asal gerilme arasındaki oran
Delta ve Dik Açılı Rozetler
Rozet gerinim ölçerler delta tip ve Dik açılı tip olarak çeşitlenirler. Bu çeşitlerdeki pul yerleşimleri yapılan bir çok hesabı basitleştirecek şekildedir.
Dik açılı Rozetler
Bu tip; birbiri ile 45o açı yapacak şekilde, X ve Y eksenlerinde birer adet olmak üzere toplam 3 gerinim pulundan oluşur (Şekil: 6). Dik açılı yerleşiminden dolayı bu tipin matematik hesapları delta’ya göre daha basittir, ancak günümüzdeki bilgisayarlar sayesinde bu hesaplama kolaylığını rozet tipi seçiminde göz önüne almayız.
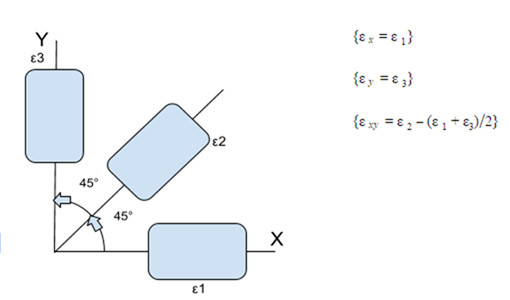
Söz konusu dokuz değeri dik açılı rozetten hesaplamak için aşağıdaki formülleri kullanabiliriz.
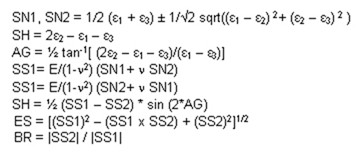
Delta Rozetler
Bu tipte pullar dik açılı rozetlere göre daha geniş bir alanı kapsarlar. Birbirleri ile 60o‘lik açı yapan gerinim pullarının ortada bulunanı Y ekseni boyunca uzanır.
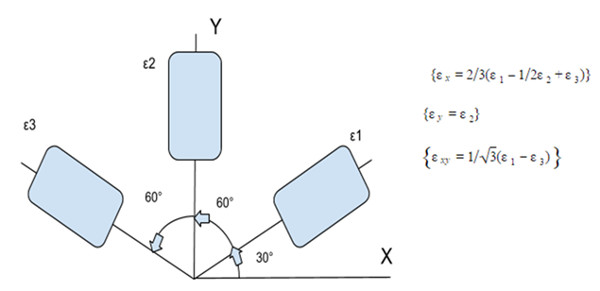
Söz konusu dokuz değeri delta rozetten hesaplamak için aşağıdaki formülleri kullanabiliriz.
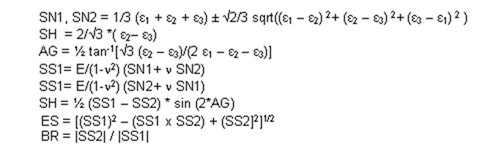
Biaxiality Ratio
Rozet hesaplamalarında, iki asal gerilmenin(SS1,SS2) oranı olan biaxial ratio da hesaplanır. Bu oran sürekli 1 ile -1 arasında olmalıdır, bu nedenle büyük olan asal gerilme her zaman payda bölümüne yazılır.
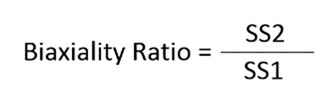
1 ile -1 arasındaki Biaxiality Ratio,
– Eğer oran 0 ise, gerilme/gerinim bölgesi tek eksende bası veya çeki şeklindedir.
– Eğer oran -1 ise, gerilme/gerinim bölgesi sadece kayma gerinimi veya gerilmesi şeklindedir.
‘Biaxilary Ratio’, LMS Test.Lab virtual channel’daki rozet hesaplamaları kullanırak hesaplanan değerlerden biridir.
LMS Test.Lab da Rozet Ölçümü
Test.Lab‘da rozet tipi gerinim pulundan ölçüm almak için; ‘Signature Acquisition’ arayüzündeki ‘Channel Setup’ sayfasının, Şekil 8’de görüldüğü üzere sağ üst köşesinden ‘Virtual Channels’ seçilir.

‘Virtual Channels’ seçildikten sonra, karşımıza Şekil 9’da görüldüğü üzere bir formül sayfası çıkar.
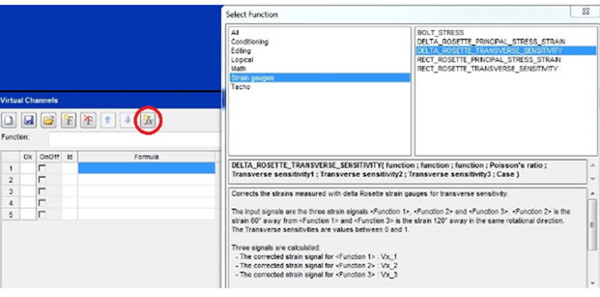
Burada, ‘f(x)’ (Insert Function) butonuna tıklanarak fonksiyon grubu olrak ‘Strain gauges’ seçilir. Ardından testte kullanılacak rozet tipi seçilir (Delta veya Rectengular).
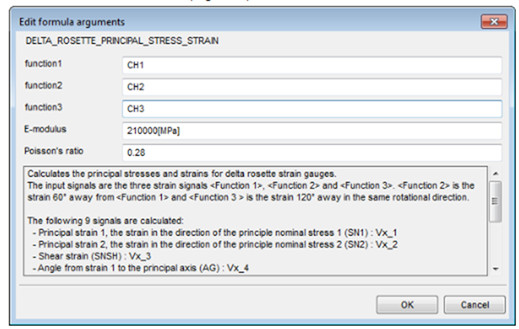
‘Edit formula arguments’ bölümünden rozette bulunan üç gerinim pulu için birer kanal, test malzemesinin young modülü ve poisson oranı girilir (Şekil 10).
‘OK’ butonuna tıklanarak ‘Edit formula arguments’ menüsü kapatılır. Yazının önceki bölümlerinde bahsettiğimiz rozet gerinim pulundan hesaplanan dokuz değer için Şekil 11’de görüldüğü üzere dokuz kanal oluşturulmuş olur.
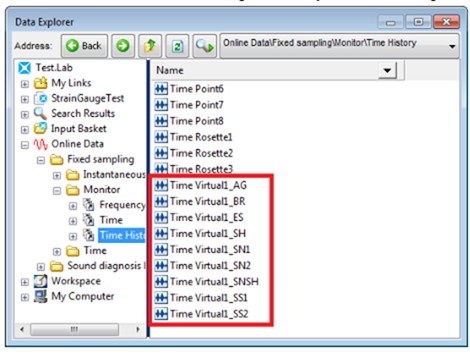
Rozet gerinim pulu hesapları, halihazırda bulunan veriler için LMS Test.Lab ‘Time Signal Calculator’ bölümünden de offline olarak da hesaplanabilir.
LMS Test.Lab, birleştirilmiş arayüzü ve değişik uygulamalar arasındaki sorunsuz veri paylaşım kapasitesiyle, standart ve tekrarlayan testleriniz için veriminizi en yüksek seviyeye çıkarmaktadır. LMS Test.Lab yazılımı ve LMS Scadas veri toplama donanımı arasındaki entegrasyon, mühendislere tüm laboratuvar ve açık alan testlerini gerçekleştirmek için tek yazılım ve donanım kullanma kolaylığı getirmiştir. Hızlı görüntüleme, güçlü analiz ve kolay raporlama özellikleri mühendislerin hızlı, eksiksiz, doğru testler gerçekleştirmelerine olanak sağlamaktadır.
Mühendislik hizmetlerimiz veya satışını gerçekleştirdiğimiz yazılımlar, sensörler ve veri toplama cihazları hakkında detaylı bilgi için lütfen DTA Mühendislik Test & Ölçüm Bölümü mühendisleriyle iletişime geçiniz.
İlgili Yazılar:
– Rainflow Çevrim Sayma Metodu
– Yapılarda Yorulma Hasarı Nasıl Hesaplanır ?