Fourier Dönüşümü, titreşim analizi, ses mühendisliği ve görüntü işleme gibi birçok alanda kullanılan önemli bir matematiksel araçtır.
Fourier Dönüşümü neden önemlidir ? Fourier Dönüşümü, zaman alanındaki bir sinyali frekans alanına dönüştürmek için kullanılır. Bu durum sinyalin anlaşılmasını kolaylaştırır.
Bu yazı Fourier Dönüşümünün kısa bir tarihini, arka planını, bazı örnekleri ve uygulamaları içermektedir.
Tarih
Fourier Dönüşümü ısı akışı analizinin başlangıcından, birçok farklı alanda yaygın kullanımına kadar, 200 yıldan daha eskidir.
Kökeni
Fourier Dönüşümü adını Fransız matematikçi Jean-Baptiste Joseph Fourier’den (Şekil 1) almaktadır. 1807’de herhangi bir fonksiyonun, sinüs ve kosinüs fonksiyonlarının toplamı olarak yazılabileceğini buldu.

Fourier, bu bulgularını Analytical Theory of Heat kapsamında 1822’de yayınlandı.
Daha sonrasında integral kullanarak,Fourier serisini oluşturan bireysel sinüs ve kosinüs dalgalarının genliğinin belirlenmesinin mümkün olduğunu keşfedildi. Bu,Fourier Dönüşümü olarak anılmaya başlandı.
Fourier Dönüşümü Dijitalleşiyor
Günümüzde yaygın olarak bilgisayar tabanlı uygulamalarda iki tip Fourier Dönüşümü kullanılmaktadır. İlki DiscreteFourierTransform (DFT) diğeri ise FastFourierTransform (FFT).
1. DiscreteFourierTransform, ayrık bir zaman bloğu üzerinde bir Fourier Dönüşümü gerçekleştirir. Bir DFT, rastgele sayıda veri noktasından oluşan herhangi bir zaman sinyalinde gerçekleştirilebilir.
2. FFT, hesaplamalı olarak verimli bir şekilde DFT gerçekleştiren bir algoritmadır. Analiz edilen zaman bloğunda ikinin katları kadar örnek gerektirir. (512, 1024, 2048).
Fourier Dönüşümünün Temelleri
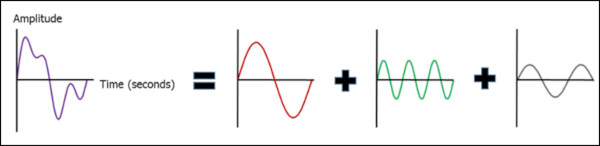
Fourier, herhangi bir sinyalin, farklı genlikteki ve fazdaki sinüs dalga serileri ile ifade edilebileceğini gösterdi. Örneğin, aşağıda gösterilen mor renkli sinyal (Şekil 2) 3 adet sinüs dalgasının toplamıdır.
Fourier Dönüşümü, orijinal zaman sinyalinin sinüzoitlere ayrılmasını mümkün kılar. Her sinüzoidin ilişkili bir genliği, fazı ve frekansı vardır. Bu, aşağıdaki Şekil 3’te gösterilmektedir.
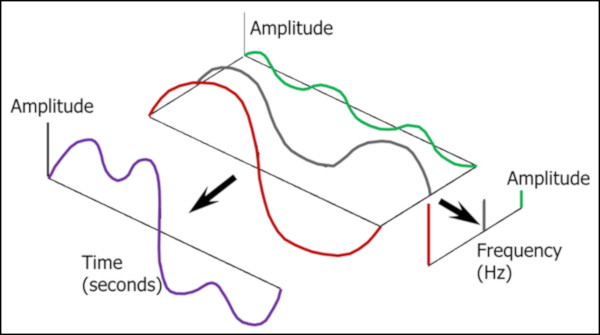
Şekil 3’te, zaman alanındaki karmaşık görünümlü bir dalga formunun, frekans alanındaki üç dikey çizgi ile temsil edilebildiği görülebilir. Frekans alanındaki bu basit gösterim, anahtar frekansların tanımlanmasına yardımcı olur.
” Fourier Dönüşümü, karmaşık zaman sinyallerini frekans bileşenlerine ayırarak kolay anlaşılmasını sağlar.”
Frekans alanından zaman alanına geçerken hiçbir veri kaybolmaz.
Fourier Dönüşümü Denklemi
Fourier Dönüşümü için analitik denklem aşağıda verilmiştir.

– Sx(f), frekans alanında Fourier Dönüşümünün çıktısıdır.
– x(t), zaman alanı fonksiyonudur.
– 2πf, saniyede radyan cinsinden frekanstır.
Karmaşık Sayılar
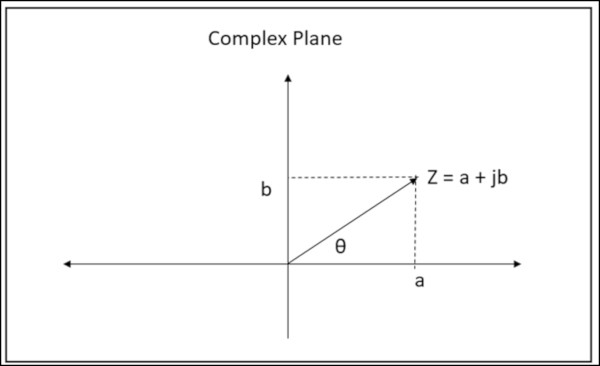
Fourier dönüşümünün çıktısı, frekans spektrumundaki bir frekansa, genliğe ve faza karşılık gelen bir dizi karmaşık sayıdır. Karmaşık sayılar a+jb formatındadır. a harfi karmaşık sayısının gerçek kısmını belirtirken, b ise imajiner kısmıdır.
Karmaşık sayılar, Şekil 4’te gösterildiği gibi orijinal zaman sinyalindeki frekans bileşenlerinin genliği ve fazı hakkında bilgi içerir. Karmaşık sayının genliği hipotenüstür. Faz θ açısıdır.
Denklem 2 ve 3, gerçek ve imajiner değerler ile genlik ve faz arasındaki ilişkiyi gösterir.

Fourier Dönüşümünün sonuçları genlik ve faz (sol grafik, Şekil 5) veya gerçek ve imajiner (sağ grafik, Şekil 5) olarak gösterilebilir.
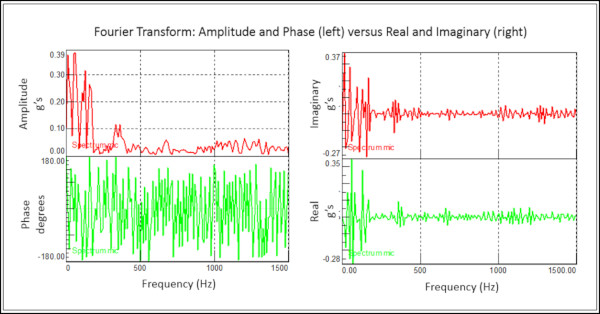
Genellikle, genlik ve faz gösterimi spektral bilgiyi görüntülemek için kullanılır.
” Fourier Dönüşümü, orijinal sinyal bileşenlerinin genlik ve faz bilgilerinin korunduğu karmaşık nümerik bir çıktıya sahiptir.”
Faz bilgisi korunduğu için, spectral verilere ters Fourier Dönüşümü uygulanarak zaman alanına dönülebilir. Eğer faz bilgisi önemli değilse veri AutopowerSpectrum olarak bilinlen fonksiyon ile hesaplanabilir.
Çift Taraflı Spektrum
Fourier Dönüşümü, Şekil 6’da gösterildiği gibi çift taraflı bir spektrum üretir.
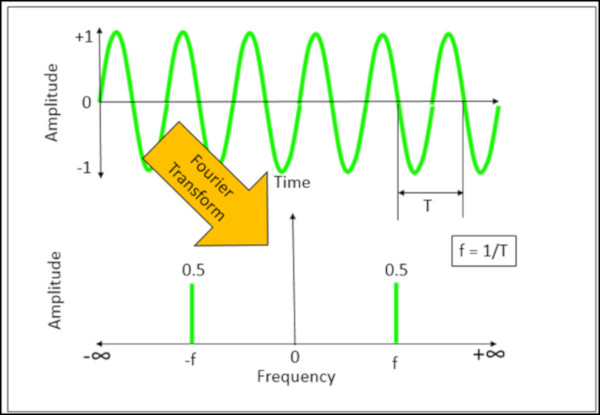
Çift taraflı spektrum negatif ve pozitif frekanslardan oluşur. Fourier Dönüşümünün analitik karşılığında zaman verisinde limitler negatif sonsuzdan pozitif sonsuza gittiği için sonuç spektrumun frekans aralığı böyledir. Çift taraflı spektrumun genliği, Şekil 6’da gösterildiği gibi zaman alanındaki tepe genliğinin yarısıdır.
Dijital veri toplama sistemleri, bir FFT veya DFT gerçekleştirirken, negatif frekans aralığını göstermez. Çift taraflı spektrumun pozitif kısmının genliği iki ile çarpılarak sonuç gösterilir. ( Genliği değişmeyen 0 Hz hariç.)
Örnek Sinyaller ve Fourier Dönüşümleri
Aşağıda zaman alanındaki bazı sinyallerin Fourier Dönüşümleri gösterilmektedir.
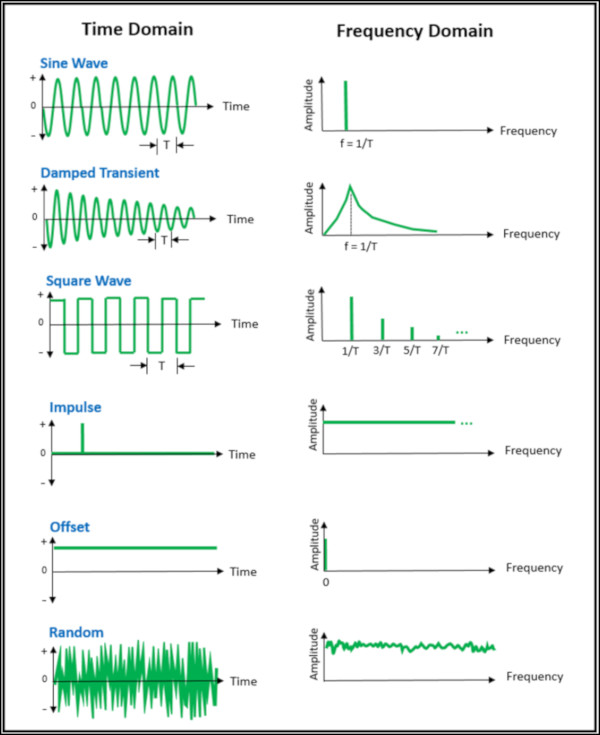
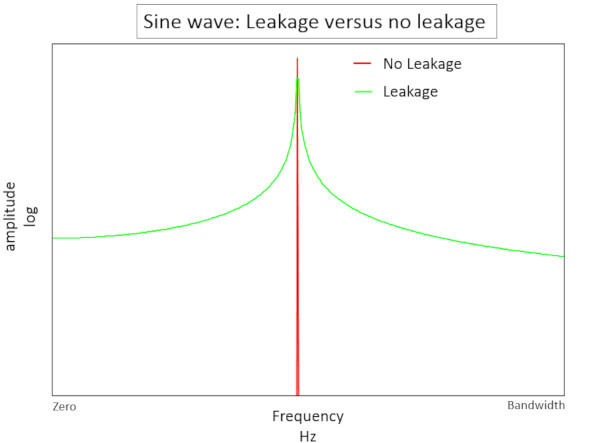
Sine Wave
Sinüs dalgası, Fourier Dönüşümünün en temel bileşenidir. Sinüs dalgasının Fourier Dönüşümü tek bir frekansta, bir faz ile tek genlik üretir.
DampedTransient
Eğer sinüs dalgasının genliği bozuluyorsa, tek frekans çevresinde bir ‘’smear’’ vardır.
Sinüs dalgasının bozulması ne kadar hızlı olursa, ‘’smear’’ o kadar geniş olur.
SquareWave
Frekans alanındaki kare dalga, genlik olarak sabit miktarda azalan tek numaralı harmoniklere sahiptir.
Impulse
Impulsive bir sinyalin Fourier Dönüşümü, frekans spektrumu boyunca düz bir genliğe sahiptir. Darbe sinyalleri genellikle modal darbe testinde kullanılır, çünkü frekans spektrumu boyunca enerjinin eşit dağılımı, bir yapının birden çok modunu uyarabilir.
Offset
Sıfır genlikten sabit bir offsetiolan bir sinyalin frekans içeriği yoktur. Ortaya çıkan Fourier Dönüşümünde, sinyalin genlik içeriği 0 Hertz’dedir.Sabit değer bir offset sinyali genellikle DC ofseti olarak adlandırılırken, dinamik frekans içeriğine sahip sinyallerin AC içeriği olduğu kabul edilir.
Random
Rastgele bir sinyalin geniş bant frekans içeriği vardır.Tüm frekanslar yaklaşık aynı seviyedeyse, spektrumun tanımlanması için genellikle White Noise terimi kullanılır.
Fourier Dönüşümünün Uygulamaları
Fourier Dönüşümü, titreşim sorunlarının giderilmesinden görüntü işlemeye kadar birçok farklı kullanıma sahiptir.
” Fourier Dönüşümü bir sinyaldeki daha yüksek frekans bileşenlerini tanımlamak için kullanılabilir. Bu bileşenler istenmeyen gürültü veya titreşimin nedenini saptayabilir.”
Bazı örnekler aşağıdadır:
Elektrikli Süpürge
Sorunlu bir elektrikli süpürgesinden toplanan zaman alanı verilerine ve ses basıncı verilerinin Fourier Dönüşümüne bakın (Şekil 8).Elektrikli süpürge çalışırken keskin, hoş olmayan bir sese sahiptir. Zaman alanında bu elektrikli süpürgeyle ilgili özel bir sorun görünmüyor.
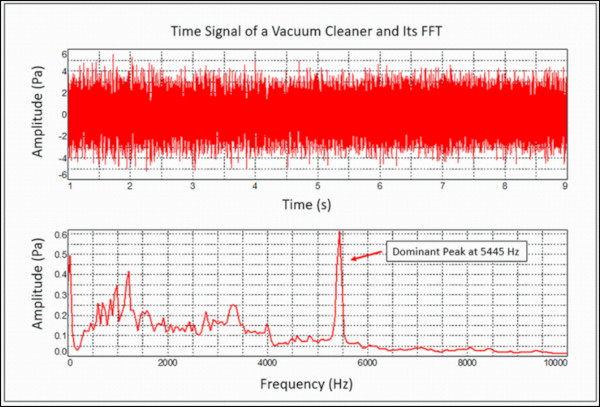
Zaman sinyalinin FFT’si 5445 Hz’de büyük bir tepe gösterir ve bu da hoş olmayan sese neden olur. Bu, fan kanadı geçişinden kaynaklanır. Mühendis, fan kanatları arasındaki mesafeyi ayarlayarak gürültülü fan sorununu çözebilir. Eşit aralıklı fan kanatları tek bir saf ton üretir. Düzensiz aralıklı bıçaklar, genliği daha düşük olan ve daha geniş bir frekans aralığında dağıtılan birden fazla ton üretecektir.
Müzik Analizi
Sesi analiz ederken, bir frekans spektrumunun genliği genellikle desibel (logaritmik bir miktar) olarak görüntülenir. Desibel, insanın ses algısının lineer genlikten daha iyi bir temsili olarak kabul edilir.
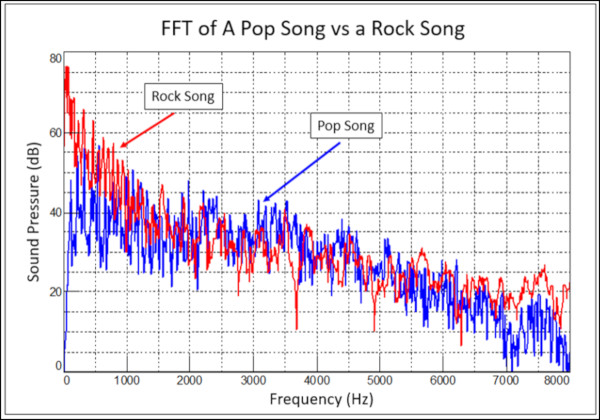
Bir rock şarkısının bir pop şarkısına karşı FourierDönüşümü’nü düşünün. Bir rock şarkısının bir pop şarkısından daha fazla bas (düşük frekans içeriği) içerdiği gösterilebilir (Şekil 9).
Rulman Hataları
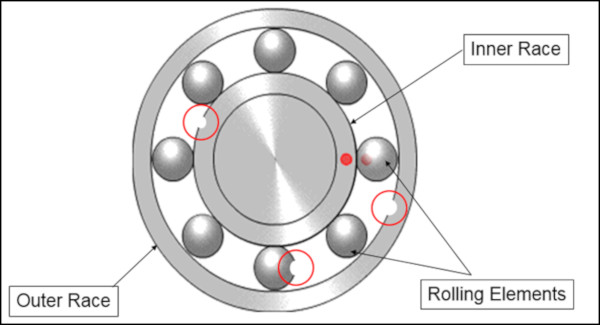
Fourier Dönüşümü, bir rulmandaki potansiyel arızayı tanımlamak için kullanılabilir. Aşağıdaki rulmanı düşünün (Şekil 10). Her bileşen (innerrace, outerrace,rollingelements) şaftın dönüşü sırasında düzenli aralıklarla birbirleriyle temas eder.Rulmanın durumu, gövdesindeki bir titreşim sensörü ile izlenebilir.
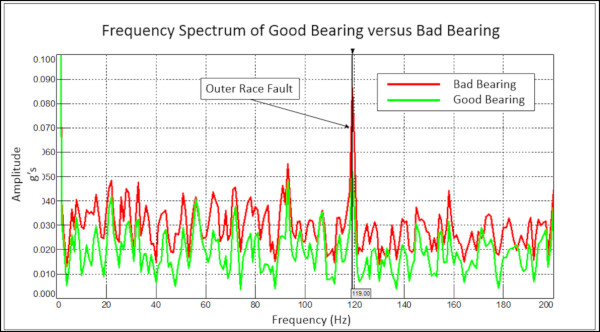
Farklı parçalar arasındaki temas belirli frekanslar üretir. Şekil 11’deki örnekte, rulmanın dış yatağı üzerindeki bir kusur 119 Hertz frekansında bir tepe üretir. Bu kusur, temel frekansa göre ilişkili frekansın titreşim genliğinin artmasına neden olur.
Rulman üreticileri genellikle her bir bileşenle ilişkili bir “arıza frekansları” tablosu sağlar, böylece yataklar kullanımdayken seviyeleri izlenebilir.
Ses Filtreleme
Fourier Dönüşümü bir sesin tonal frekans bileşenlerini tanımlayabilir. Bu tonlar daha sonra dinleyicinin deneyimini geliştirmek için filtrelenebilir. Örneğin, 2010 Dünya Kupası’nda birçok taraftar vuvuzela adlı bir enstrümanı (Şekil 12) yanlarında stadyuma getirdi.

Vuvuzela çalındığında, birçok TV izleyicisinin sinir bozucu bulduğu 235 Hz’lik bir ses çıkarır. Vuvuzela’nın frekans içeriği Fourier Dönüşümü kullanılarak tanımlandı ve daha sonra izleme deneyimini geliştirmek için bazı yayıncılar tarafından filtrelendi.
Motor Gürültüsü ve Titreşimi
Gürültü ve titreşim sorun gidermede, Fourier Dönüşümü yararlıdır. Çünkü dönen makinelerdeki birçok bileşenin benzersiz bir harmonik imzası vardır. İçten yanmalı motorlar, krank mili dengesizliği, kayış tokası, dişli çıngırağı ve yanma olayları gibi istenmeyen titreşimlere neden olabilecek birçok farklı bileşene sahiptir (Şekil 13).
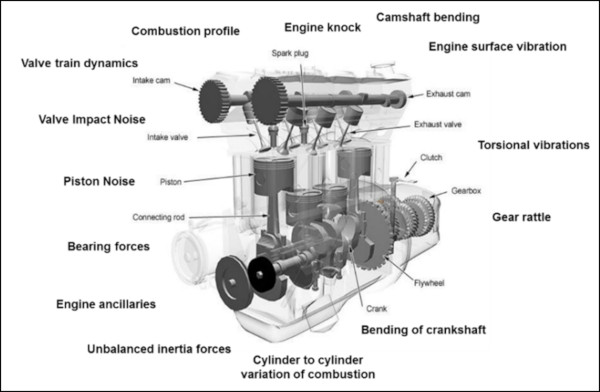
Motor bloğuna monte edilen bir ivmeölçerden alınan zaman verileri üzerinden yapılanFourier Dönüşümü, aşırı titreşime neden olan bileşenleri tanımlamak için kullanılabilir.Bir motorun hızı değiştiği için, Fourier Dönüşümleri genellikle farklı RPM’lerde yapılır ve bir renk haritasında gösterilir (Şekil 14).
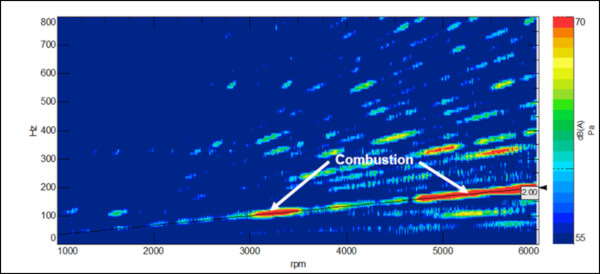
Şekil 14’teki renk haritasındaki en yüksek ses seviyeleri, motor tarafından üretilen yanma olaylarından / frekanslarından kaynaklanmaktadır. Yanma ile ilişkili frekans rpm ile değişir. Dönen şaftın RPM’i ile ilgili frekansına ‘order’ denir.
İlgili Diğer Blog Yazılarımız;
– Spectrum ve Autopower Fonksiyonları
– Dijital Sinyal İşleme: Örnekleme Frekansı, Bant Genişliği, Spektral Çizgi
Uygulama hakkında sorularınız için DTA Mühendislik Test Bölümü mühendisleriyle iletişime geçebilirsiniz.