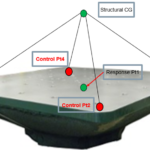
Deneysel modal analizde, bir yapı üzerinden FRF (frekans cevap fonksiyonu) seti toplanarak, bir dizi anlamlı mod şekli ve bunların ilişkili olduğu modal parametreler çıkartılır;
• Doğal Frekans
• Sönüm Değeri
• Mod Şekli
FRF’lerden bu bilgilerin çıkartılması işlemine, modal eğri uydurma ya da modal parametre tahmini denir.(Şekil 1)
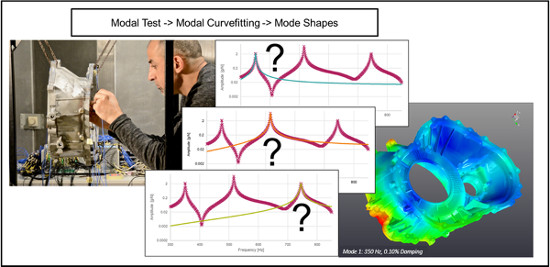
SIEMENS Simcenter Testlab ile eğri uydurma işlemi aşağıdaki işlem adımları ile yapılmaktadır;
1. Arkaplan Gürültüsü
2. XY Veri Seti Analojisi
3. Simcenter Modal Analiz Yazılımı:
– FRF ve bant genişliği
– Stabilizayon diyagramı
– Modal şekil hesaplama
– Modal validasyon
4. Tekrarlanan Kökler: Aynı frekansta 2 Mod
Arkaplan Gürültüsü
Modal eğri uydurma işleminde dikkat edilmesi gereken birkaç nokta vardır (Görsel 2) :
– FRF’lerden yapıdaki doğru doğal frekansların sayısı nasıl belirlenir? Tahmin edilen modların az veya çok olduğunu nasıl belirleriz?
– FRF’deki bir tepe noktasının ölçüm gürültüsü mü yoksa gerçek bir rezonans mı olduğunu nasıl anlarız?
– FRF’deki tepe noktaları birbirlerine çok yakınsa, tek bir tepe noktası şeklinde görünüyorsa, bu bitişik modlar matematiksel olarak birbirinden nasıl ayrılır?
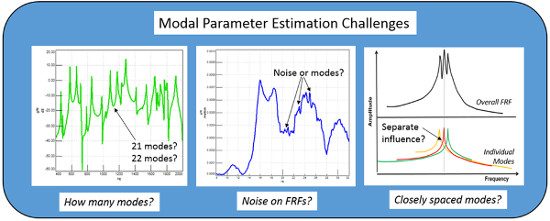
Modal eğri uydurma esnasında yukarıdaki zorlukların önüne geçebilmek için, Simcenter Testlab Modal Analysis yazılımı kullanılabilir. Stabilizasyon Diyagramı yardımıyla FRF setini tanımlayan en iyi matematiksel modal parametreler (frekanslar, sönümleme vb.) belirlenebilir.
Simcenter Testlab yazılımını detaylandırmadan önce, aşağıdaki eğri uydurma analojisi, eğri uydurma sürecini daha iyi anlamamıza yardımcı olabilir.
XY Veri Seti Analojisi
Şekil 3’de gösterildiği gibi X ve Y data seti kullanılarak eğri uydurma prosesi görselleştirilebilir.
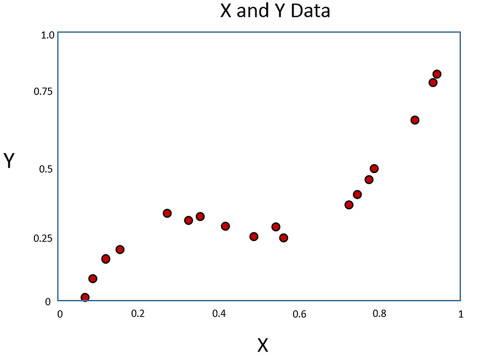
Amaç, X ve Y verilerini en iyi tanımlayan bir eğri hesaplamaktır.
Veri noktalarına bakıldığında, noktaların üçüncü dereceden bir polinom gibi görünen, matematiksel bir ilişkiye sahip olduğu görülmektedir. Ancak tüm veri noktaları polinom üzerinde yer almamaktadır.
XY veri setinden bir eğri oluşturulduğunda, veri noktaları üçüncü dereceden bir polinoma göre biraz farklılık göstermektedir. Bu farklılık, tıpkı veri toplarken elde edilen gürültü gibidir.
Veriyi matematiksel olarak en iyi şekilde temsil etmek aşağıdaki yaklaşım kullanılabilir;
1. Farklı mertebelere sahip polinomlar denemek. Örneğin; verileri önce birinci dereceden bir polinom eğrisi, sonra ikinci dereceden bir polinom ve daha sonra üçüncü dereceden bir polinom ile temsil etmek.
2. Matematiksel deklem ile veri noktaları arasındaki farkı (veya hatayı) en aza indiren polinomların mertebesini ve katsayıları bulmak.
Şekil 4’den Şekil 7’ye kadar, 1. dereceden 10. Dereceye oluşturulan polinomlar görselleştirilmektedir.
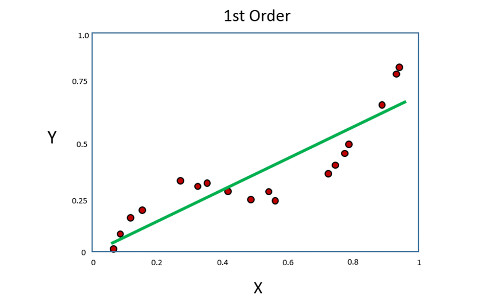
Şekil 5’de gösterilen, birinci dereceden polinom eğrisini göz önünde bulunduralım.
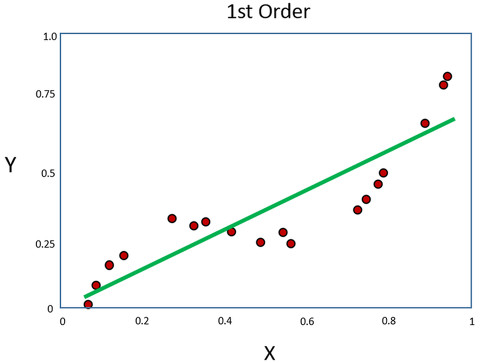
Birinci dereceden polinom, XY verilerinin genel eğilimini izlemektedir, ancak veri noktalarını mükemmel şekilde temsil etmemektedir. Eğri ve veri noktalar arasındaki farkı en aza indirmek için eğri parametreleri (eğim ve ofset) hesaplanır.
Veri noktalarını daha iyi temsil etmesi için daha yüksek dereceli bir polinomun gerekmektedir. Polinomun derecesini üçe yükselterek, Şekil 6’da gösterildiği gibi verilere daha iyi uyan bir polinom elde edilebilir.
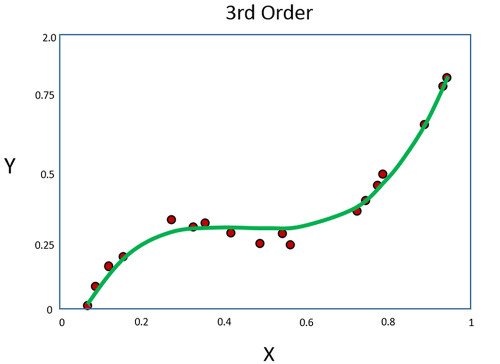
XY verilerinde, polinoma uymayan noktalar bulunmakta ve bu da polinom eğrisinin tüm veri noktalarından geçmesini imkansız hale getirmektedir.
Polinomun derecesi daha da artarsa ne olur? Şekil 7’de 10. dereceden polinomun veriler ile uyumu gösterilmektedir.
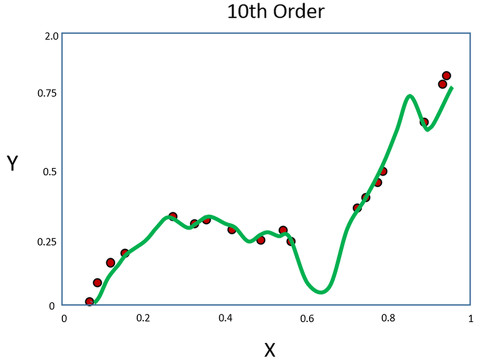
Onuncu dereceden polinomun veri noktaları ile eğri arasındaki mesafeye bağlı olarak hesaplanan hata, daha düşük dereceli polinomlara göre iyi olabilir: çünkü eğri, veri noktalarının çoğundan geçmektedir. Bununla birlikte, oluşturulan polinomun noktalar ile olan uyumunun iyi olmadığı görülmektedir. – eğride üçüncü dereceden polinoma göre şeklinden sapan bazı büyük sıçramalar bulunmaktadır.
Eğri uydururken aşağıdaki hususlar göz önünde bulundurulmalıdır;
– Polinomun derecesini arttırmak, sonucu iyileştirmektedir.
– Herhangi bir eğri uydurma metodu, verilerindeki gürültüyü ve diğer varyasyonları gidermelidir.
– Verileri analiz eden kişi, uydurulan matematiksel eğriyi doğru bir derece ile belirlemelidir.
Şimdi bu polinom analojisini Simcenter Testlab Modal Analysis kullanarak, gerçek FRF verilerinden eğri uydurmak için kullanabiliriz.
Simcenter Testlab Modal Analiz ile Modal Eğri Uydurma
Ölçülen FRF’lerden iyi bir modal parametre seti tahmin etme süreci, XY veri analojisiyle benzerlik göstermektedir:
– Ölçülen FRF’lerde, kullanılan ekipmanlardan kaynaklı elektriksel gürültü, küçük yapısal lineersizlikler, ivmeölçerlerin kaydırılması gibi, bir çok ölçüm gürültüsü yer almaktadır.
– Yapı üzerindeki farklı konumlardan elde edilen FRF’ler dikkate alınmalıdır. (Şekil 8)
– İlgilenilen frekans aralığındaki birçok mod ( doğal frekans, sönüm, mod şekli) dikkate alınmalıdır.
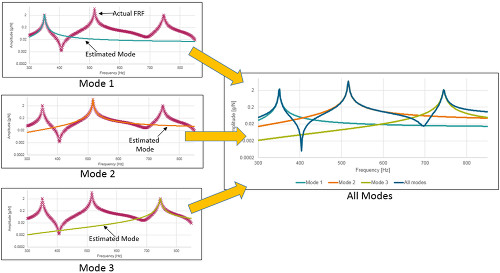
Ayrıştırılması gereken çok sayıda bilinmeyen ve dikkate alınacak birçok FRF veri noktası vardır. Model eğri yazılım ve algoritmaları ile aşağıdaki işlem adımları takip edilir;
– Test edilen yapı için belirli bir frekans aralığında doğru mod sayısını belirlenir.
– Ölçülen FRF’lerden doğal frekans, sönüm ve diğer modal bilgileri belirlenir.
– Hesaplanan modlar ve ölçülen FRF verileri arasındaki hata en aza indirilir.
– Verilerdeki gürültü azaltılır.
– En son oluşturulan modal model üzerinde, herhangi uygun olmayan bir modun olup olmadığı değerlendirilir.
Analiz yapan kişinin sonuçları manuel olarak incelemesi ve yukarıdakilerin hepsinin uygun şekilde yapıldığından emin olması gerekecektir.
Süreç
Simcenter Testlab Modal Analysis yazılımında modal eğri uydurma işlem adımları Şekil 9’da gösterilmektedir .
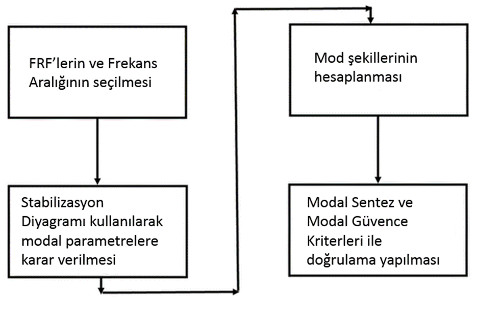
Tatmin edici bir eğri elde edilinceye kadar bu işlemin tekrarlanması gerekebilir. Sürecin ilk üç adımı Simcenter TestLAB Modal Analiz çalışma sayfasında yer alan Polymax veya Time MDOF ile yapılır. Doğrulama adımları, Modal Synthesis ve Modal Validation ile yapılır.
Polymax, Simcenter Modal Analysis yazılımında (Tools -> Add-ins -> Modal Analysis and Polymax Modal Analysis) aracılığıyla açılır. Modal eğri uydurma işleminde, çoğunlukla Polymax algoritması kullanılmaktadır.
Seçilen FRF’ler ve Frekans Aralığı
Şekil 10’da gösterildiği gibi, Modal eğri uydurmanın ilk adımı, analiz edilecek FRF seti ve frekans aralığını belirlemektir.
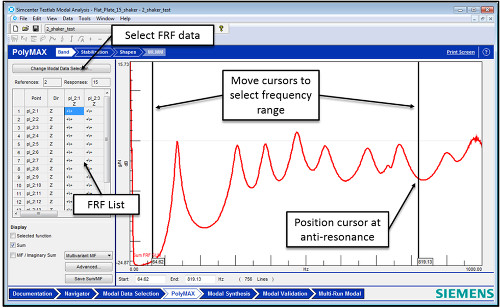
Bant genişliği seçim penceresinin bazı önemli özellikleri:
- FRF Seçimi – FRF seçimi ekranın sol üst kısmından yapılır. Varsayılan olarak, mevcut proje bölümünün tüm ölçümleri kullanılır. Aynı isimdeki FRF’ler mevcutsa, sadece en son ölçüm kullanılır. Eğer kötü bir FRF ölçümü elde edilmişse, örneğin zayıf tutarlılıkla (coherence), problemin kaynağı tespit edilerek bu FRF ölçümü tekrarlanır. Ardından yeniden elde edilmiş FRF, eğri uydurma işlemine katılır.
- Bant Genişliği Seçimi – Analiz edilecek frekans aralığı çift imleç kullanılarak seçilir. Genelde, imleçleri düşük ivme yanıtlı veya anti-rezonans bölgesine yerleştirmek en iyi yöntemdir, böylece modal bilgiler kesilmemiş olacaktır.
- Veri Görselleştirme Yerleşimi – Çalışma sayfasının sol alt köşesinde, kullanıcının eğri uydurma işlemi sırasında ekranda gösterilecek FRF işlevlerini seçmesine izin verir. “Selected Function” seçimi bireysel ölçümlerin gösterilmesine izin verirken, “Sum” ölçülen tüm FRF’lerin ortalamasını göstermektedir.
Ekranda gösterilen (Şekil 10) bu toplam FRF eğrisi, analiz için bant genişliğinin seçilmesine yardımcı olmak amaçlı yanlızca görselleştirme içindir. Analizde tüm FRF’ler kullanılacaktır. Analiz edilen FRF’lerin tam listesi ekranın sol tarafında gösterilir.
Stabilizasyon Diyagramı
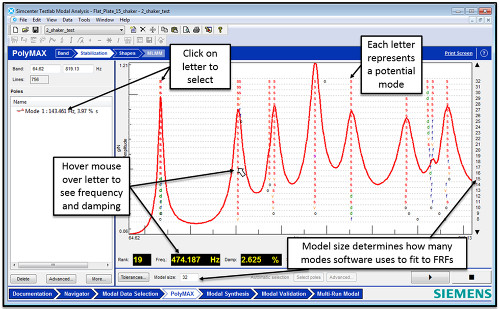
Stabilizasyon diyagramı, her biri harf içeren birçok satıra sahiptir:
- Satır Numarası – Ekranın sağ tarafındaki sayılar, yazılım algoritmasının FRF verilerini tanımlamak için kullandığı iterasyon sayısını (önceki XY data analojisinden gelen polinomun derecesi gibi) temsil eder.
- Harfler – Her satırdaki harfler, ölçülen FRF’leri analiz ederek, yazılımın belirlediği potansiyel modları temsil eder. Harf tipi, modal tahminin kalitesini gösterir.
Stabilizasyon Diyagramı Satırları
Her satırdaki harf sayısı veya potansiyel modlar, satır numarasını asla aşmaz ( Şekil 12 ). Simcenter Testlab anlamsız mod seçimlerini göstermeyeceğinden, satırlardaki harf sayısı, satır sayısından az olabilir. Örneğin, eğri uydurma algoritması tarafından negatif frekanslı veya negatif sönümlemeli bir potansiyel mod tanımlanmışsa, gösterilmez.
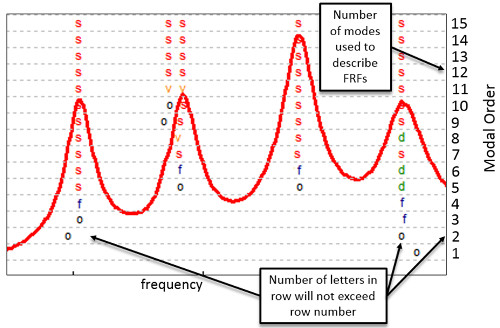
Potansiyel modu temsil eden harf, üzerine tıklanarak eğri uyumu analizi için seçilebilir.
Stabilizasyon Diyagramı Harfleri
Harfler, belirli bir potansiyel model çözümünün tekrarlanabilirliğini gösterir. Bu, mevcut satırdaki potansiyel çözümler (frekanslar, sönümler, vb.), Şekil 13’te gösterildiği gibi önceki satırdaki potansiyel çözümler ile karşılaştırılarak yapılır .
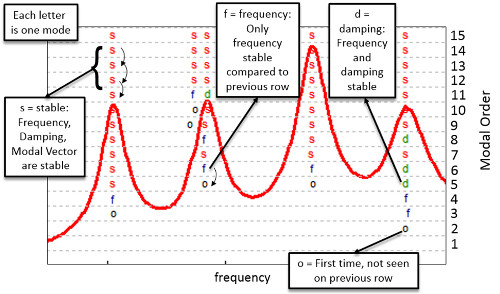
Harfleri yazmak ile çözümlerin istikrarı, işaret ler en tekrarlanabilir olma.
• o- Yeni: Bu çözümün bir önceki satırda mevcut olmadığı anlamına gelir.
• f – Frekans: Potansiyel modun frekansı bir önceki satıra göre dengelenirse, f harfi kullanılır.
• d – Sönümleme: Hem frekans hem de sönümleme değerleri önceki satıra göre dengelenirse d harfi kullanılır.
• v – Vektör: Frekans ve modal katılım vektörünün her ikisi de stabilize edilmiş ise v harfi kullanılır.
• s – Kararlı: Modal çözüm, frekans, sönümleme ve modal katılım vektöründe tamamen dengelenmiş ise s harfi ile gösterilir.
İdeal olarak, s harflerinin sütunları modların varlığını gösterir (Not: 50 veya 60 Hz’de çok güçlü bir s harfi sütunu olsa bile, çok hafif bir şekilde sönümlenen bir mod, test nesnesinin bir modu değil, muhtemelen elektriksel gürültüdür).
Harflerin bulunduğu sütunlardan yanlızca bir s harfini seçmek, çözüm tekrarlanabilir olduğundan yeterli olacaktır.
Stabilizasyon Diyagramı Toleransları
Sonuçlar ne kadar tekrarlanabilir? Çözümün dengelemesi için toleransların belirlenmesi ekranının sol alt köşesinde “Tolerances…” butonu ile yapılır. Bu ekranda, harf atamaları için kullanılan tolerans yüzdeleri değiştirilebilir. ( Şekil 14 ).
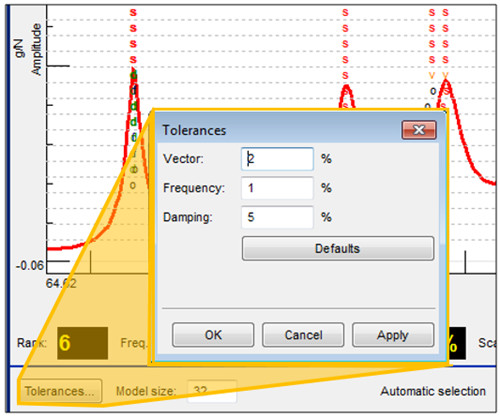
Örneğin, doğal frekans için değişkenlik % 0.1’e kadar ayarlanabilir.
Mod Şekillerinin Hesaplanması
En iyi potansiyel mod grubunu seçtikten sonra, bir sonraki adım, Şekil 15’te gösterildiği gibi mod şekillerini hesaplamaktır . Ekranın sol üst köşesindeki “Shapes” küçük çalışma sayfasına tıklanır.
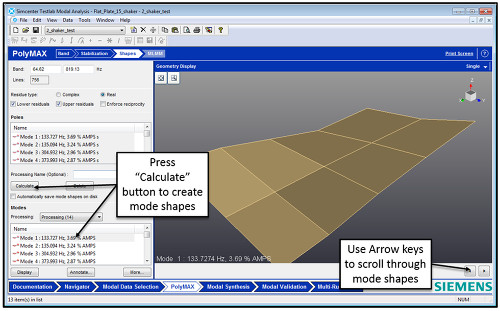
Modal şekilleri belirlemek için ekranın sol kısmında yer alan “Calculate” düğmesine basılır. Hesaplanan modal şekiller sol altta listelenir. Mod şekilleri, bu kısımdan geometri üzerine sürükleyerek veya sağ alt taraftaki oklar kullanılarak görüntülenir.
Modal Model Doğrulama
Hesaplanan mod şekilleriyle, bazı doğrulama adımları kullanılarak sonuçlar iki kez kontrol edilebilir. Bu şekilde hiçbir modun kaçırılmaması ve çok fazla modun dahil edilmesi önlenebilir.
Yaygın olarak kullanılan iki doğrulama yöntemi vardır: Modal Sentez ve Modal Güvence Kriteri . Bu yöntemler iki ayrı çalışma sayfasında yer almaktadır.
Modal Sentez: Cevapsız Modların Kontrolü
Hesaplanan mod seti kullanılarak, hesaplanan FRF’ler ölçülen FRF’lerle karşılaştırılabilir.
Bunu yaparken, Şekil 16’da gösterildiği gibi modların analiz dışında bırakıldığı hataları yakalamak çoğu zaman mümkündür .
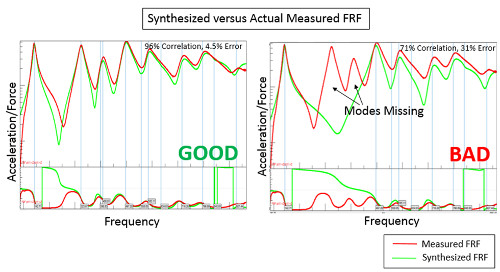
Ölçülen her FRF bu şekilde kontrol edilebilir. Her FRF için bir korelasyon ve hata yüzdesi hesaplanır ve gösterilir. Korelasyon yüzdesinin mümkün olduğunca yüksek, %100’e yakın olması arzu edilirken, hata yüzdesinin düşük olması, mümkün olduğunca sıfıra yakın olmalıdır.
Analizde eksik olan modlar varsa, Stabilizasyon adımına geri dönülerek analize eklenmelidir.
Modal Güvence Kriteri: Çok Fazla Modu Kontrol Etme
İyi bir modal senteze sahip olunsa bile çok fazla mod seçilmiş olabilir. Modal Güvence Kriteri bu durumun belirlenmesini sağlar.
Modal Güvence Kriteri (MAC) iki mod şeklini karşılaştırır. Modlar birbirine benziyorsa, MAC değeri % 100’e yakın olacaktır. Farklı olan iki mod ise % 0’a yakın bir MAC’ye sahip olacaktır.
İdeal olarak, modal parametre tahmini sırasında tanımlanan her modun kendine özgü mod şekline sahip olması gerekir.
Çok fazla mod nasıl seçilebilir? İki farklı modal eğri uyarlama algoritması için Stabilizasyon Diyagramını gösteren Şekil 17’yi dikkate alın : Time MDOF ve Polymax.
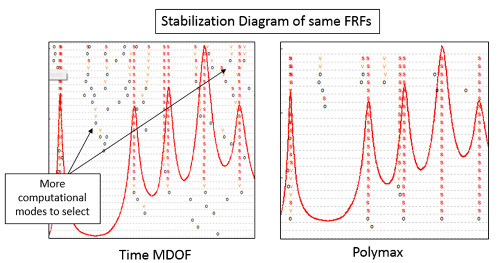
Bir kullanıcının Time MDOF stabilizasyon şemasında ( Şekil 17’nin sol tarafı ) ekstra bir mod seçmesi kolay olacaktır. Ekstra veya yinelenen bir mod seçildiğinde, seçilen modun şekli, yakındaki modlara çok benzeyecektir. Benzer mod şekilleri fiziksel olarak imkansızdır: Her mod şekli benzersiz olmalıdır. Modal arasındaki bu benzerlik, Şekil 18’de gösterildiği gibi yüksek bir MAC değeri olarak işaretlenecektir .
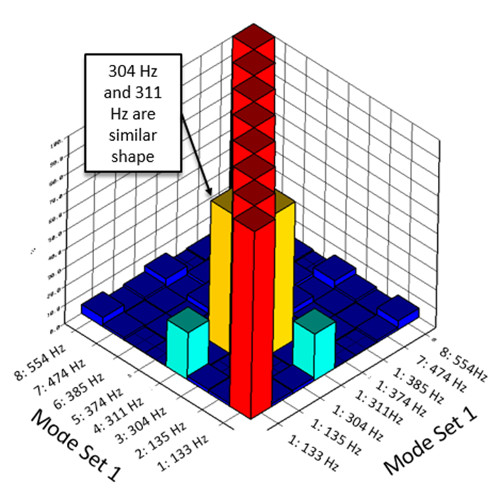
Yukarıdaki şekil, 304 Hz modunun ve 311 Hz modunun muhtemelen aynı mod olduğunu göstermektedir. Modlardan birinin seçimi kaldırılmalıdır.
Tekrarlanan Kökler: Aynı Frekansta İki Mod
Birçok yapıda, aynı frekansta iki modun bulunması mümkündür. Bu genellikle simetrik yapılarda (tüpler, diskler vb.) görülmektedir.
Bir yapının tekrarlanan bir kökü olup olmadığını belirlemek için, Mode Indicator Function (MIF) kullanılır. Aynı frekansta iki mod varsa ve iki MIF varsa, her MIF, Şekil 19’da gösterildiği şekilde, aynı frekansta iki modun varlığına işaret edecek şekilde düşüş gösterir (mavi eğri).
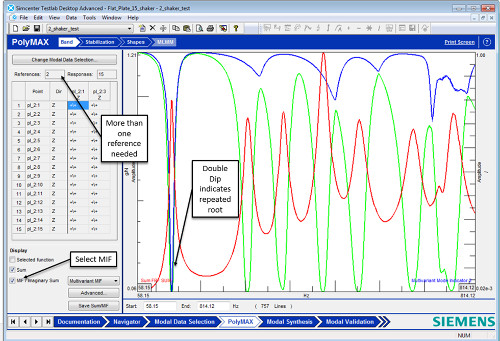
Mode indicator function, iki modun olduğu frekanslarda “azalır”. Şekil 19’da , mavi ve yeşil MIF eğrisi aynı frekansta azalmaktadır. Bu düşüş, aynı frekansta iki modun varlığını gösterir.
Matematiksel olarak, hem birincil hem de ikincil mod gösterge fonksiyonuna sahip olmak için iki referansa sahip olmak gerekir.
Son olarak, Modal Modelin Maksimum Olabilirlik tahminini (MLMM) kullanılarak, toplanan FRF verileriyle daha iyi eşleşme yapabilmek için frekanslarda ve sönümlerde otomatik ayarlamalar yapılabilir.
SIEMENS Simcenter Testlab yazılımları hakkındaki sorularınız için lütfen DTA Mühendislik Test Bölümü mühendisleriyle iletişime geçiniz.