Bir Wöhler eğrisi (bazen S-N eğrisi olarak yazılır), belirli bir malzeme için hasara neden olacak çevrim sayısı ile gerilme büyüklüğünün bir grafiğidir. Tipik olarak, hem gerilme hem de çevrim sayısı logaritmik ölçeklerde gösterilir.
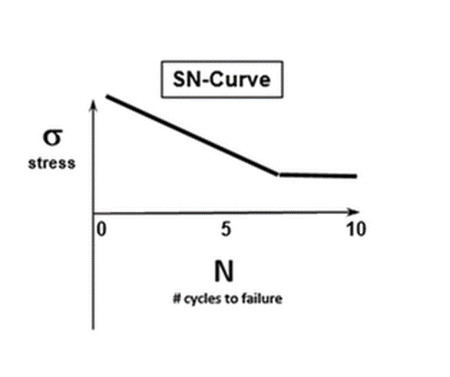
Bir yükleme zaman geçmişi ve bir Wöhler eğrisi göz önüne alındığında, mekanik bir parçanın biriken hasarı veya yorulma ömrünü belirlemek için Miner Kuralı kullanılabilir.
Tarih
Wöhler eğrisi, Fransa’nın Versailles kentinde 1842 yılında meydana gelen tren kazasının sonucu olarak, Alman bilim adamı August Wöhler (Şekil 1) tarafından geliştirildi. Bu kazada, demiryolundaki günlük tekrarlanan “düşük seviye” çevrimsel gerilmeden dolayı tren lokomotifinin aksı kırıldı.
Wöhler, araştırma yaparken aks yüzeyinde çatlakların oluştuğunu ve yavaşça büyüdüğünü keşfetti. Çatlakların, kritik bir boyuta ulaştıktan sonra aniden yayıldığını ve aksın kırıldığını buldu. Bu yüklerin seviyesi, aksı üretmek için kullanılan malzemenin çekme dayanımından ve/veya akma dayanımından daha az olmuştur.
Wöhler, demiryolu akslarına tekrarlanan yükleri uygulamak ve yük seviyesi ile tekrarlanan çevrim sayısı arasındaki ilişkiyi çizebilmek için bir cihaz geliştirdi. “Wöhler eğrileri”, alternatif/çevrimsel gerilim seviyelerinin, hasara neden olabilecek kadar çevrim sayısı ile ilişkisini çizer.
Bir lokomotifin ağırlığını taşıyabilecek, ilk statik yüke dayanacak bir aks tasarlamak iyi anlaşılmıştı. Bir aksın hemen çökmemesi durumunda bir trenin ağırlığını taşıyabileceği oldukça açıktır. Uzun süre tekrarlanan düşük seviyeli çevrimsel gerilme kavramı nispeten yeniydi ve iyi anlaşılamamıştı. O zamanlar birçok gözlemci için bir aksın ne zaman hataya uğrayacağı tahmin edilemez gözüküyordu. Bu durum, Wöhler’in çevrimsel gerilmelerin daha iyi anlaşılabileceği Wöhler eğrilerini geliştirmesiyle son buldu ve yorulma ömrü daha tutarlı bir şekilde tahmin edilebilir hale geldi.
Belirli bir malzeme için Wöhler eğrisi nasıl oluşturulur?
Günümüzde bu eğriler metal kupon test makinesi kullanarak geliştirilmektedir. Küçük bir metal kupon, makineye yerleştirilir ve metal kuponda bir çatlak veya arıza meydana gelinceye kadar döngüsel (veya alternatif) bir gerilmeye maruz kalır.
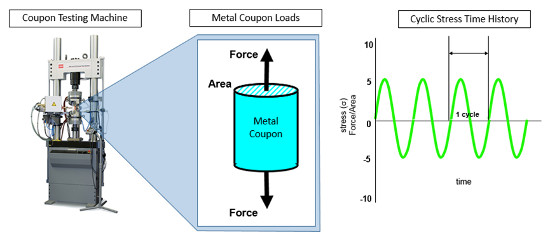
Birçok kupon, Wöhler eğrisini geliştirmek için farklı gerilme seviyelerinde test edilmelidir. Şekil 3 metal kupon testinden türetilmiş klasik bir Wöhler eğrisini göstermektedir.
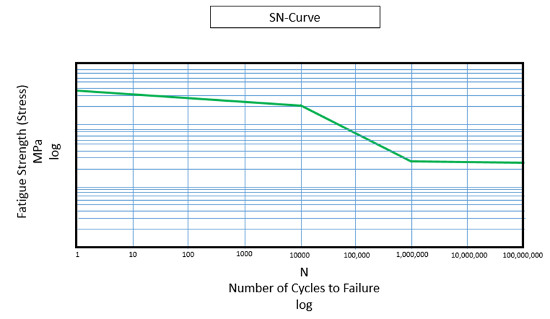
Bir Wöhler eğrisi, alternatif gerilme seviyesi ile hasarın oluştuğu çevrim sayısı arasında bir “arama tablosu” işlevi görür (Şekil 4). Çoğu Wöhler eğrisi genellikle sol üstten sağ alt kısma doğru eğimlidir. Bu durum, yüksek seviyeli genlik çevrimlerinin, düşük seviyeli genlik çevrimlerine kıyasla hasara karşı daha az sayıda çevrim sayısına sahip olduğunu gösterir.
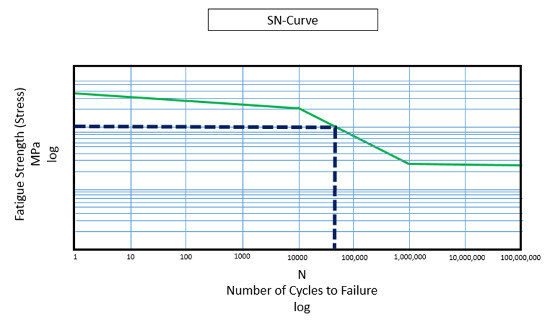
Bunun gibi bir yorulma testinde, çevrimlerin uygulandığı frekans, hasar için çevrim sayısında bir faktör olarak kabul edilmez.
Wöhler eğrisi sonuçlarını etkileyen çevrim sayısıdır, çevrimlerin uygulanma hızı değil.
Gerçek hayatta, çevrimlerin frekansı, özellikle yükleme frekansı, nesnenin doğal bir frekansı veya rezonansı ile çakışıyorsa, bir faktör olabilir.
Plastik, Elastik ve Sonsuz Ömür Bölgeleri
Bir Wöhler eğrisi farklı alanlar içerebilir: Şekil 5’te gösterildiği gibi plastik bölge, elastik bölge ve sonsuz ömür bölgesi.
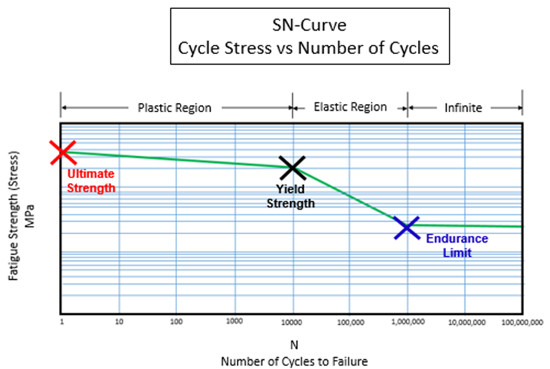
Plastik, elastik ve sonsuz yaşam bölgelerini ayıran 3 anahtar kavram vardır:
- Çekme Dayanımı: Bir çevrimde hasara uğraması için gereken gerilme seviyesi
- Akma Dayanımı: Elastik ve plastik bölgeyi ayırma noktası
- Yorulma Sınırı: Tüm çevrimler bu gerilme seviyesi genliğinin altındaysa, hiçbir hasar meydana gelmez
Wöhler eğrisi üzerindeki değerlerin birçoğu, bir malzeme kuponu üzerinde statik bir gerilme-gerinim testi yapılarak bulunabilir (bakınız Şekil 6).
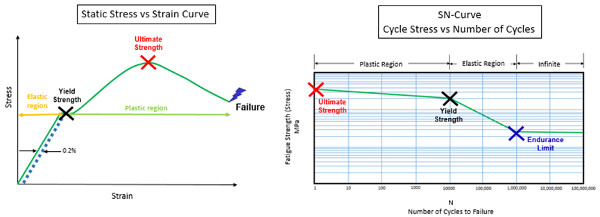
Örneğin Çekme Dayanımı gerilme değeri malzemenin bir çevrimde hasara uğradığı noktadır. Akma Dayanımı ise plastik ve elastik bölgeyi ayıran noktadır.
Sonsuz Ömür
Çelik gibi bazı malzemeler sonsuz ömür bölgesi sergilerler (Şekil 7). Bu bölgede, gerilme değerleri belirli seviyenin altındaysa, hasara neden olmadan sonsuz sayıda çevrim uygulanabilir (elbette, gerçek hayatta sonsuz sayıda döngü için hiçbir test yapılmamıştır, ancak bir milyon + çevrim tipiktir).
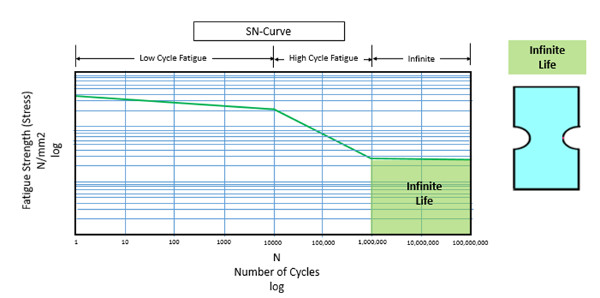
Kritik bileşenler (örneğin motor krank mili ve kolları) genellikle sonsuz ömre sahip olacak şekilde tasarlanırlar. Çünkü çevrimler hıza bağlıdır ve hızlı bir şekilde birikirler. Parçanın maruz kaldığı tüm çevrimsel gerilme seviyeleri sonsuz ömür için yorulma sınırının altında olmalıdır.
Belirli koşullar altında sonsuz ömür geçerli değildir:
- Sonsuz ömür sadece gerilme çevrimlerinin sayısına dayanır, korozyonu ve başka faktörleri göz önünde bulundurmaz.
- Çevrimsel gerilme seviyelerinden herhangi biri daha yüksekse ve plastik veya elastik bölgede ise, yorulma sınırı artık geçerli değildir.
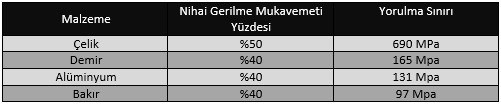
Farklı metallerin farklı yorulma sınırları vardır. Bazı tipik yorulma sınırları tablo 1’de gösterilmektedir.
Alüminyum, magnezyum ve bakır alaşımları gibi birçok demir dışı metal ve alaşım, iyi tanımlanmış yorulma sınırları göstermez (Şekil 8).
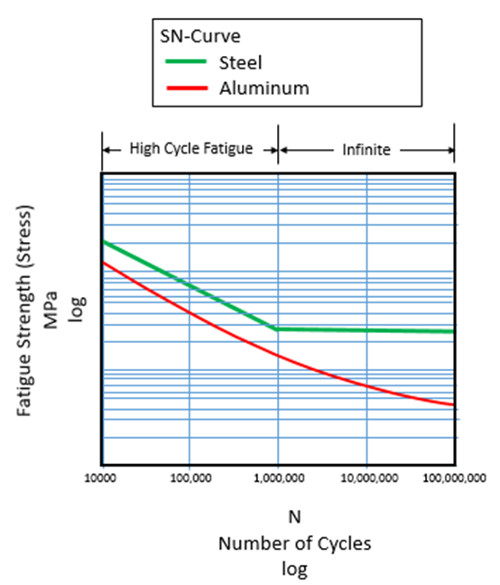
Çeliğin yorulma sınırındaki eğiminde kesin bir değişime sahip olduğu durumlarda, alüminyum ve diğer metallerin her zaman belirgin bir değişikliği olmaz.
Sonsuz ömür bölgesinde bir parçanın veya nesnenin çalışıp çalışmadığını belirlemek için genellikle Goodman-Haigh diyagramı kullanılır. Çevrim genliğine ek olarak, ortalama gerilme Goodman-Haigh yaklaşımında da açıklanmaktadır.
Elastik Bölge
Elastik bölgede (Şekil 9), gerilme ve gerinim arasındaki ilişki lineer kalır. Bir çevrim uygulandığında ve kaldırıldığında, malzeme orijinal şekline ve/veya uzunluğuna döner. Bu bölge ayrıca “Yüksek Çevrimli Yorulma” (High Cycle Fatigue) bölgesi olarak adlandırılır. Çünkü düşük genlikteki çok sayıda gerilme çevrimi parçanın bozulmasına neden olabilir.
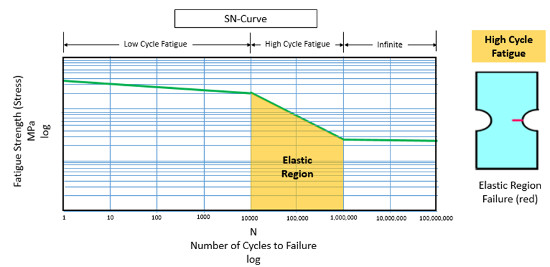
Elastik bölgedeki bir malzemenin performansını etkileyen tipik faktörler artık gerilmeler ve geometrik faktörlerdir. Örneğin, malzemedeki ciddi bir geometri değişikliğinin yumuşak bir geometri değişikliğinden ziyade bir çatlak başlatma olasılığı daha yüksek olabilir.
Plastik Bölge
Plastik bölgede (Şekil 10) malzeme, yüksek gerilme seviyelerine maruz kalmaktadır, bu da tekrarlanan gerilme çevrimlerinin uygulanması nedeniyle şekil ve / veya geometrinin değişmesine neden olmaktadır. Ayrıca bu bölge yüksek genliğe sahip düşük sayıda gerilme çevriminin hataya yol açtığı “Düşük Çevrimli Yorulma” (Low Cycle Fatigue) bölgesi olarak adlandırılmaktadır.
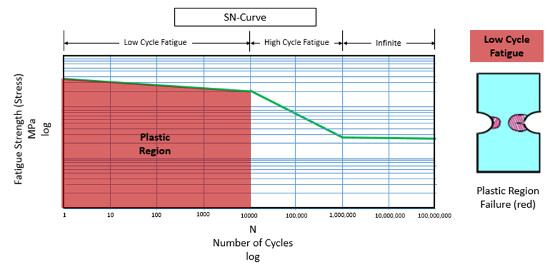
Malzeme plastisitesi ve geometrisi, plastik bölgedeki hataya neden olabilecek çevrim sayısı üzerindeki büyük etkilerdir.
Wöhler eğrisi ile bir malzemenin plastik bölgesindeki yorulma ömrünün veya hasarının hesaplanması çok iyi bir yöntem değildir. Çevrimsel gerilme seviyeleri plastik bölgede ise, analizin bir parçası olarak bir E-N (Gerinim – Çevrim Sayısı) içeren bir gerinim ömrü yaklaşımı tipik olarak tavsiye edilir. Gerinim ömrü, yüklerin uygulanma derecesini veya sırasını da dikkate alır.
Wöhler Eğrisi Kütüphaneleri
Malzeme testlerinin yapılması pahalı olabilir. İdeal olarak, testler birçok kez ve birçok farklı gerilme seviyesinde tekrarlanmalıdır. Yeterli deneylerle Wöhler eğrisi, Şekil 11’de gösterildiği gibi ana eğri etrafında bir dizi güven aralığından oluşacaktır.
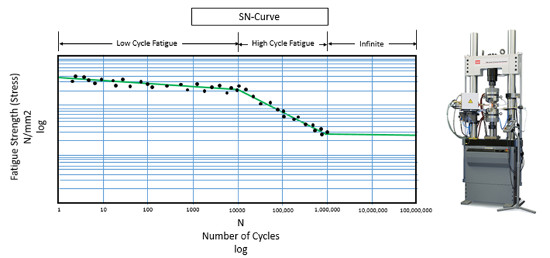
Bazı malzemeler iyi bilinen eğrilere sahiptir çünkü kullanımları çok yaygındır. Yeni bir alaşım geliştirildiğinde, Wöhler eğrisi tamamen bilinmeyebilir ve bunu belirlemek için test gerekebilir. Geleneksel olarak, Wöhler eğrisini belirlemek için her seviyede üç tekrarlı beş farklı gerilme seviyesi minimum olarak kabul edilir. “FKM Analytical Strenght Assesment” kitabı birçok malzeme için Wöhler eğrisini içermektedir. Bu kitap Siemens’i içeren bir mühendislik şirketi olan VDMA (Verband Deutscher Maschinen- und Anlagenbau e.V.) tarafından yayınlanmıştır.
Wöhler Eğrisinin Logaritmik Doğası: Çift genlikli ve Çift çevrim örneği
Hasar açısından değerlendirilecek aşağıdaki varsayımsal çevrimleri göz önünde bulundurun:
- 1000 çevrim için 300 MPa’lık Alternatif Gerilme
- 2000 çevrim için 300 MPa’lık Alternatif Gerilme
- 1000 çevrim için 600 MPa’lık Alternatif Gerilme
Zaman geçmişi #1 ve zaman geçmişi #2 Şekil 12’te gösterilmektedir. Bu zaman geçmişleri şunları içerir:
- Aynı genlikte çevrimler
- Farklı çevrim sayıları
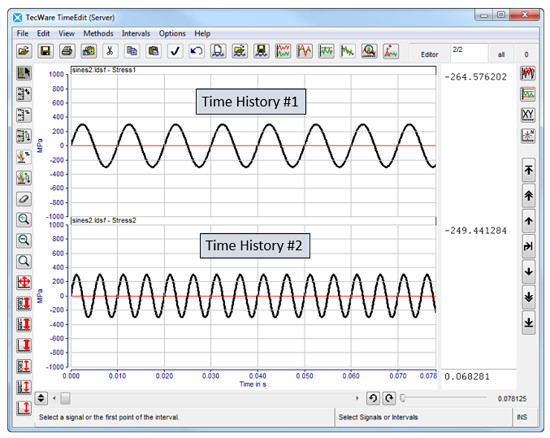
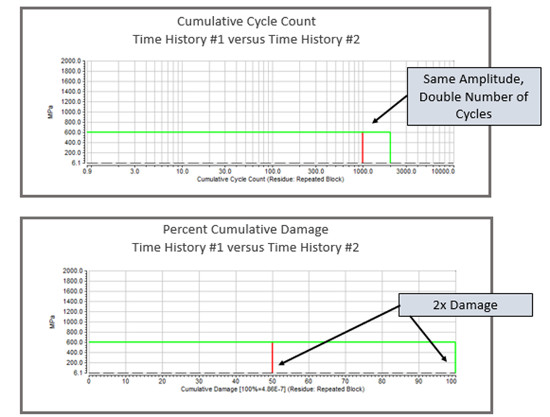
Miner Kuralı kullanılarak, zaman geçmişi #2’nin kümülatif hasarının zaman geçmişi #2 ile karşılaştırıldığında iki katı olduğu görülür (bkz. Şekil 13).
Daha sonra, Şekil 14’te gösterilen zaman geçmişi # 1 ve zaman geçmişi # 3’teki hasar potansiyelini karşılaştırın. Bu zaman geçmişleri şunları içerir:
- Farklı genlikte çevrimler
- Aynı sayıda çevrim
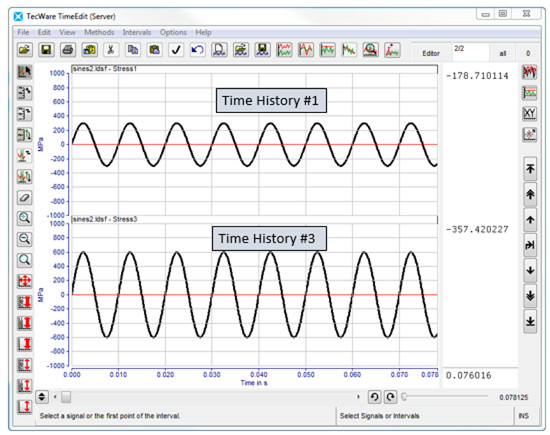
Bir Wöhler Eğrisi ile yükleme zaman geçmişini analiz etmek için Miner Kuralını kullanarak, çevrimlerin genliği sadece iki kat olsa bile, zaman geçmişi #3’ün kümülatif hasarının zaman geçmişi # 1’e (Şekil 15) kıyasla 20 kat olduğunu görülür.
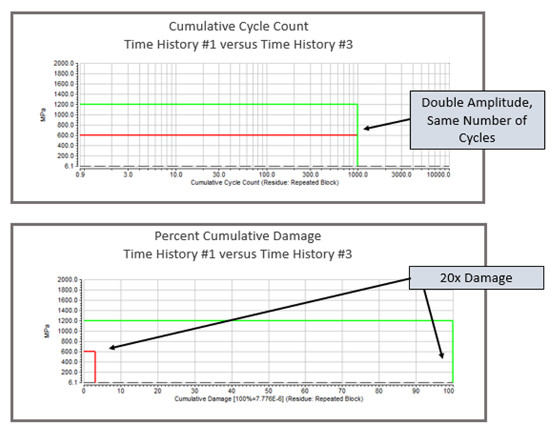
Gerilme seviyesinin iki katına çıkarılması neden yirmi kat hasara sebep olur? Bunun nedeni Wöhler eğrisi aslında log-log grafiğidir.
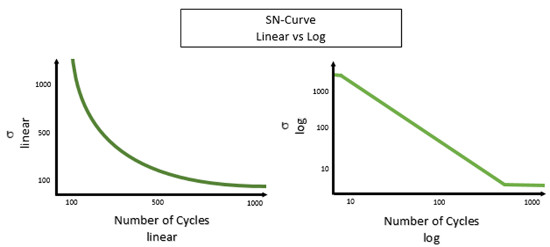
Yorulma ömrü için çok önemli etkileri olan gerilme seviyesi ve hasara sebep olabilecek çevrim sayısı arasındaki ilişki doğrusal değildir.
Wöhler Eğrisinin Eğimi: K-Faktörü
Logaritmik ölçekli Wöhler eğrisinin eğimi k-faktörünü verir. Bu “k-faktörü”, gerilme seviyesi ile hasara neden olabilecek çevrim sayısı arasındaki ilişkiyi yönetir.
“K-faktörü” Wöhler tarafından yük (yani gerilme) ile ömrü (hasara sebep olabilecek çevrim sayısı) kolayca ilişkilendirmek için geliştirilmiştir. Şekil 17, Wöhler eğrisinin k-faktörü kullanılarak malzeme ömrünü nasıl etkilediğini göstermektedir.
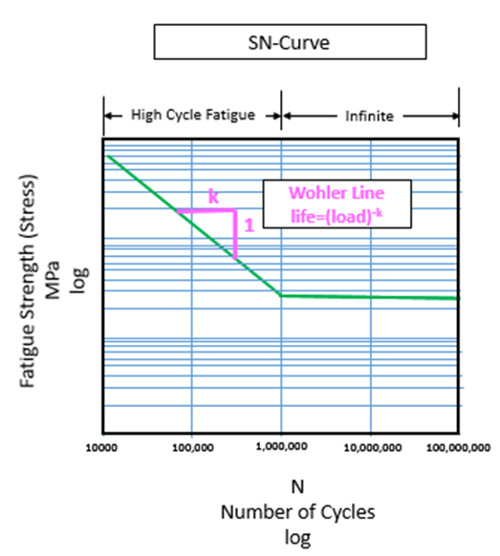
Bu logaritmik ölçeklendirme nedeniyle, yük genliğindeki küçük bir değişikliğin yorulma ömrü veya hasarında çok büyük bir değişiklik olabileceği anlamına gelir. Aşağıda gösterilen Tablo 2’de k faktörü 5 olduğunda yükteki %15’lik bir değişim, yorulma ömründe 2 kat değişikliğine neden olmaktadır.

Alternatif gerilme seviyesi ile hasara sebep olabilecek çevrim sayısı arasındaki logaritmik ilişki, yorulma testinin hızlandırılmasında önemli bir husustur. K faktörü büyüdükçe yükteki küçük artışlar (yani gerilme) malzemenin ömründe daha büyük değişiklikler yaratır. Bu durum, bir dayanıklılık (Durability) testini hızlandırmak için kullanılabilir. Yükü az miktarda artırarak test süresinde büyük düşüşler elde edilebilir.
Genel bir kural olarak, k faktörlerini aşağıdaki gibi ilişkilendirilebilir:
• 7 K faktörü: Alüminyum
• 5 K faktörü: Çelik
• 3 K faktörü: Kaynaklar
Ortalama Gerilmeye Bağlı Wöhler Eğrisi Ayarlamaları
Wöhler eğrileri kullanırken, eğrinin belirli durumları yansıtacak şekilde ayarlanması gereken koşullar olabilir.
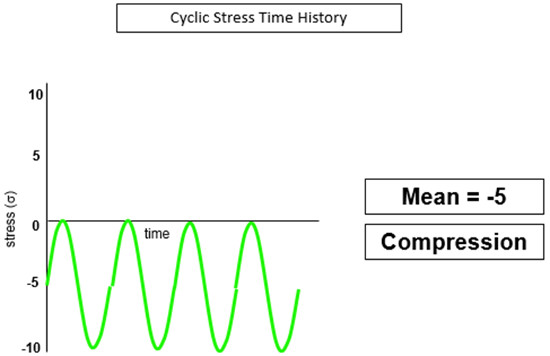
Şekil 18’deki gerilme zaman geçmişini düşünelim. Çevrimlerin ortalama gerilimi sıfırdır.
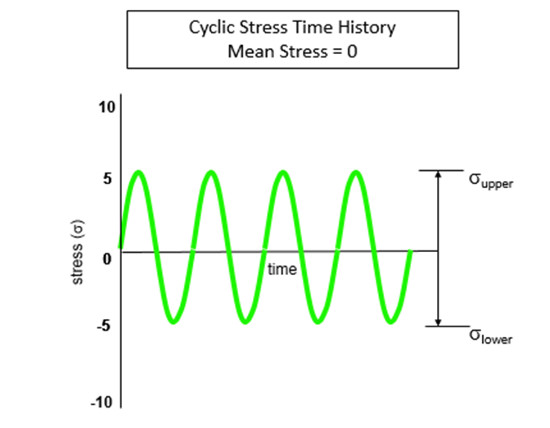
Neden ortalama gerilmeyi takip etmeliyim? Gerçek yükleme durumlarında, parçaya etki eden ortalama gerilme sıfırdan farklı olabilir. Örneğin, bir arabanın süspansiyon sistemi, arabanın statik ağırlığını (veya yükünü) taşımak zorundadır. Araç yolda giderken, araç ağırlığı ortalama bir gerilme uygularken (sıfır olmayan) yoldaki çarpmalarla çevrimsel gerilmeler / yükler uygulanır.
Bir parçanın karşılaşabileceği iki farklı ortalama gerilme türü vardır: çekme (tension) ve basma (compression).
Çekme durumunda (Şekil 19), pozitif bir ortalama gerilme vardır. Metal kupon testinde, statik çekme gerilme ortalaması kuponu kırmaya çalışan bir yük oluşturur.
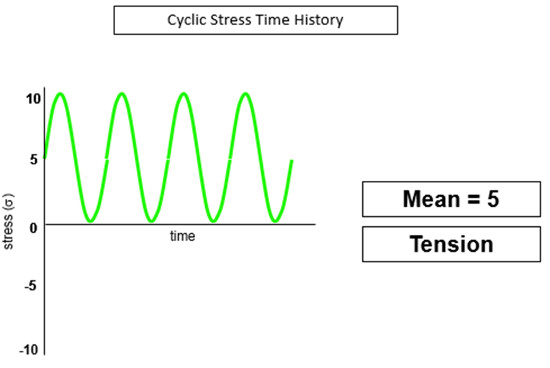
Bu ek çekme, hasara sebep olabilecek çevrim sayısını azaltır. Parça, sıfır gerilim ile tahmin edilen Wöhler eğrisinden daha erken hasara uğrar.
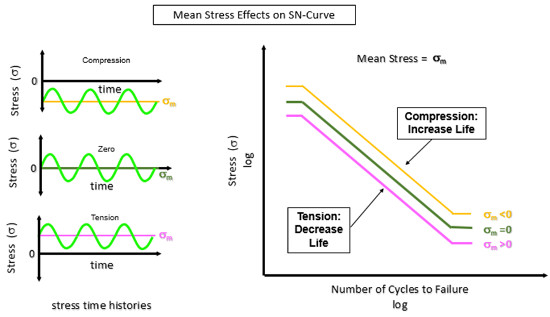
Statik ortalama gerilme de basma yaratarak parçayı bir arada tutmaya çalışabilir (Şekil 20). Bu basma, parçanın ömrünü uzatarak, ortalama gerilmenin sıfır olduğu durumdaki Wöhler eğrisinin tahmin edebileceği ömründen daha uzun sürmesini sağlayacaktır.
Ortalama gerilme, Wöhler eğrisini etkin bir şekilde yukarı veya aşağı kaydırır (Şekil 21). Çekme ortalama gerilmesi Wöhler eğrisini aşağıya doğru kaydırır, böylece daha az sayıda çevrimin hatalı olması gerekir. Basma ortalama gerilmesi, Wöhler eğrisini yukarı doğru kaydırır, böylece hataya sebep olabilecek çevrim sayısı daha fazladır.
Tipik olarak Wöhler eğrileri, Şekil 22’de gösterildiği gibi spesifik bir “Gerilme Oranı” için geliştirilmiştir. R olarak adlandırılan “gerilme oranı”, gerilmenin düşük değerinin, çevrimsel gerilme zaman geçmişindeki gerilmenin üst değerine bölünmesiyle elde edilir. Wöhler eğrisi testi koşullarını belirlemek için bu uygun bir yoldur. Örneğin, havacılık ve uzay endüstrisinde, birçok bileşen, malzeme üzerinde net bir çekme sağlayan 0,1 gerilme oranıyla test edilir.
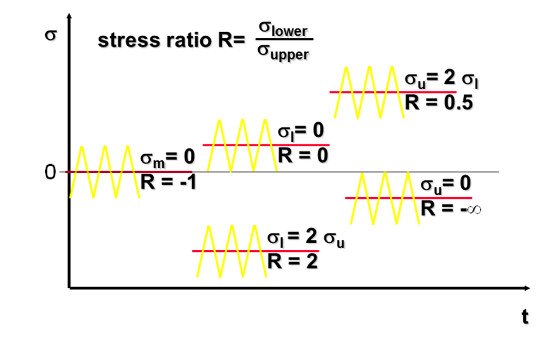
Ortalama gerilmesi 0 olan, tam tersine çevrilmiş yükleme koşulları için, R, -1’e eşittir. Statik yükleme için, R değeri 1’e eşittir. Ortalama gerilmenin pozitif ve gerilme genliğine eşit olduğu bir durumda, R değeri 0’a eşittir.
Yükleme Nedeniyle Wöhler Eğrisi Ayarlamaları
Yükün yapıya nasıl uygulandığı, hasara sebep olabilecek çevrim sayısında bir fark yaratır. Yük, çeşitli şekillerde uygulanabilir: Şekil 23’te gösterildiği gibi burulma, bükme, eksenel vs.

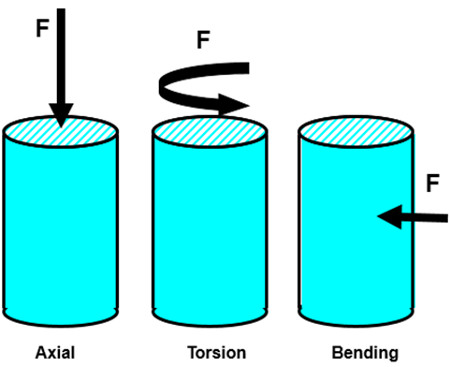
Yük ölçeklendirme düzeltme faktörleri (Cf) farklıdır ve malzemeye bağlıdır. Düzeltme faktörleri, uygulanan yük tipine bağlı olarak gerilmeyi arttırmak veya azaltmak için kullanılır. Şekil 23’teki malzeme için bükme ve burulma durumları arasındaki düzeltme % 40’tır.
Diğer Wöhler Eğrisi Ayarları
Bir Wöhler eğrisinin ayarlanması gerekebileceği başka birçok neden daha vardır. Diğer Wöhler eğrisi ayarlamaları parça boyutu, yüzey kaplamaları, geometrideki çentikler vb. olabilir.
Uygulama hakkında sorularınız için DTA Mühendislik Test Bölümü mühendisleriyle iletişime geçebilirsiniz.